题目内容
16．
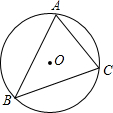如图，已知△ABC的外接圆O的半径为3，AC=4，则sinB=$\frac{2}{3}$．
分析 作直径AD，连接CD，根据正弦的概念求出∠D的正弦，根据圆周角定理得到∠B=∠D，得到答案．
解答 解：
作直径AD，连接CD，
在直角△ADC中，AD=6，AC=4，
sinD=$\frac{AC}{AD}$=$\frac{4}{6}$=$\frac{2}{3}$，
∵∠B=∠D，
∴sinB=$\frac{2}{3}$，
故答案为：$\frac{2}{3}$．
点评 本题考查的是圆周角定理和解直角三角形的知识，正确作出辅助线、构造直角三角形是解题的关键，注意锐角三角函数的概念的运用．
练习册系列答案
相关题目
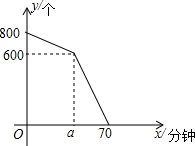在妇女节前后，某快递总站的快递数量不断增加，每个快递到达总站后都需要进行快递单号的扫描，妇女节当天的早上，快递总站在进行快递单号扫描前，已收到800个未扫描快递，在扫描机开始工作后，仍平均每分钟有10个未扫描快递到达快递总站，扫描机平均每分钟扫描15个快递单号．已知在扫描机开始工作a分钟内只用一台扫描机工作．在妇女节当天未扫描的快递个数y（个）与扫描机工作时间x（分钟）之间的关系如图所示．
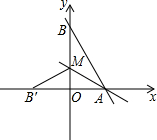如图，直线y=-$\frac{4}{3}$x+8与x轴，y轴分别交于点A和B，M是OB上的一点，若将△ABM沿AM折叠，点B恰好落在x轴上的点B′处，则△AMO的面积为9．
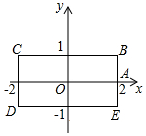如图，长方形BCDE的各边分别平行于x轴或y轴，物体甲和物体乙分别由点A（2，0）同时出发，沿长方形BCDE的边作环绕运动，物体甲按逆时针方向以1个单位/秒匀速运动，物体乙按顺时针方向以2个单位/秒匀速运动，则两个物体运动后的第2015次相遇地点的坐标是（ ）
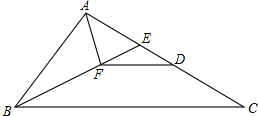推理填空：完成下列证明：如图，E在△ABC的边AC上，且∠ABF=∠C，AF平分∠BAE交BE于点F，FD∥BC交AC于D．求证：AC-AB=DC．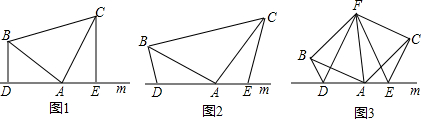
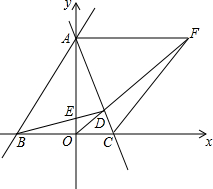如图，在平面直角坐标系中，直线AB与直线AC分别交于x轴，y轴于点B、C、A，过点B作BD⊥AC于D，交y轴与点E，若∠BAC=45°，点B、C、E的坐标分别B（-3，0）、C（2，0）、E（0，1），过点A作AF∥x轴，交OD的延长线于点F，连接CF，在平面直角坐标系中，是否存在点K，使△OKF与△OCF全等？若存在，求出点K的坐标并画出图形；若不存在，说明理由．
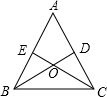如图，在△ABC中，点D，E分别在边AC，AB上，BD与CE交于点O，给出下列四个条件：①∠EBO=∠DCO；②BE=CD；③OB=OC；④OE=OD．从上述四个条件中，选取两个条件，不能判定△ABC是等腰三角形的是（ ）