题目内容
19．
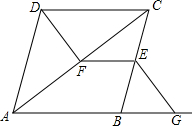如图，在菱形ABCD中，E、F分别是BC、AC上的点，G是AB延长线上的一点，且EF∥CD，∠BEG=∠CDF，求证：DF=EG．
分析 连结BF，根据菱形的性质，通过SAS证明△CDF≌△CBF，根据全等三角形的性质得到DF=BF，∠CBF=∠CDF，根据等量代换得到∠BEG=∠CBF，根据平行线的判定得到BF∥EG，根据平行线的判定得到四边形EFBG是平行四边形，再根据平行四边形的性质和等量代换即可求解．
解答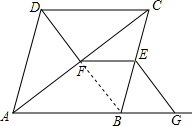 
证明：连结BF，
∵四边形ABCD是菱形，
∴CD∥AB，CD=CB，∠BCF=∠DCF，
在△CDF与△CBF中，
$\left\{\begin{array}{l}{CD=CB}\\{∠BCF=∠DCF}\\{CF=CF}\end{array}\right.$，
∴△CDF≌△CBF（SAS），
∴DF=BF，∠CBF=∠CDF，
∵EF∥CD，
∴EF∥AG，
∵∠BEG=∠CDF，
∴∠BEG=∠CBF，
∴BF∥EG，
∴四边形EFBG是平行四边形，
∴BF=EG，
∴DF=EG．
点评 考查了菱形的性质，同时利用了全等三角形的判定和性质，平行线的判定，平行四边形的判定和性质，综合性较强，有一定的难度．．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
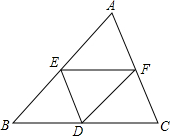如图，E和F分别是边AB和AC中点，D是BC边上一点，若∠AED=∠AFD，请问四边形AEDF是平行四边形吗？为什么？
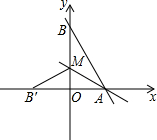如图，直线y=-$\frac{4}{3}$x+8与x轴，y轴分别交于点A和B，M是OB上的一点，若将△ABM沿AM折叠，点B恰好落在x轴上的点B′处，则△AMO的面积为9．
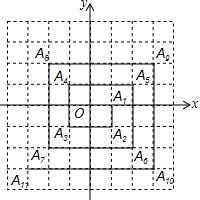如图，已知A1（1，0），A2（1，-1），A3（-1，-1），A4（-1，1），A5（2，1），…，则点A2014的坐标是（504，-504）．
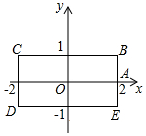如图，长方形BCDE的各边分别平行于x轴或y轴，物体甲和物体乙分别由点A（2，0）同时出发，沿长方形BCDE的边作环绕运动，物体甲按逆时针方向以1个单位/秒匀速运动，物体乙按顺时针方向以2个单位/秒匀速运动，则两个物体运动后的第2015次相遇地点的坐标是（ ）