题目内容
18.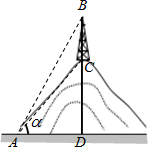 课外兴趣小组要在操场上借助侧倾器测量学校对面小山CD的高度.在A处测得山顶电信塔顶B处的仰角∠β=60°,塔脚C处的仰角∠α=45°.已知电信塔高BC=21米,求山高CD.(参考数据:$\sqrt{2}≈1.4,\sqrt{3}≈1.7,\sqrt{5}≈2.2$)
课外兴趣小组要在操场上借助侧倾器测量学校对面小山CD的高度.在A处测得山顶电信塔顶B处的仰角∠β=60°,塔脚C处的仰角∠α=45°.已知电信塔高BC=21米,求山高CD.(参考数据:$\sqrt{2}≈1.4,\sqrt{3}≈1.7,\sqrt{5}≈2.2$)
分析 设山高CD为x米,根据直角三角形的性质得到AD=x,根据正切的概念列出算式计算即可.
解答 解:设山高CD为x米,
∵∠α=45°,
∴AD=x,
tan∠BAD=$\frac{BD}{AD}$,即$\frac{x+21}{x}=\sqrt{3}$,
解得,x=$\frac{21(\sqrt{3}+1)}{2}$≈28.4米,
答:山高CD为28.4米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角和俯角的概念、正确运用锐角三角函数的概念是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.抛物线y=-2x2-1的对称轴是( )
| A. | 直线x=$\frac{1}{2}$ | B. | 直线x=-$\frac{1}{2}$ | C. | y轴 | D. | 直线x=2 |
10.已知函数:①y=3x-1;②y=3x2-1;③y=-20x2;④y=x2-6x+5,其中是二次函数的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.已知,一组数据x1,x2…x9的平均数为5,方差为2,则数据2x1+1,2x2+1…2x9+1的平均数和方差分别为( )
| A. | 5、4 | B. | 6、2 | C. | 11、4 | D. | 11、8 |
 如图,在梯形ABCD中,AD∥BC,S△AOD:S△BOC=1:9.
如图,在梯形ABCD中,AD∥BC,S△AOD:S△BOC=1:9. 如图,一艘轮船从距离灯塔C处80海里的A处向正东航行,并测得C在A的北偏东60°方向,则轮船按这条路线航行过程中离灯塔的最近距离是40海里.
如图,一艘轮船从距离灯塔C处80海里的A处向正东航行,并测得C在A的北偏东60°方向,则轮船按这条路线航行过程中离灯塔的最近距离是40海里.