题目内容
7．若⊙P的半径为5，圆心P的坐标为（3，4），则平面直角坐标系的原点O与⊙P的位置关系是在圆上．分析 先根据勾股定理求出OP的长，再与⊙P的半径为5相比较即可．
解答 解：∵圆心P的坐标为（3，4），
∴OP=$\sqrt{{3}^{2}+{4}^{2}}$=5．
∵⊙P的半径为5，
∴原点O在⊙P上．
故答案为：在圆上．
点评 本题考查的是点与圆的位置关系，熟知点与圆的三种位置关系是解答此题的关键．
练习册系列答案
孟建平名校考卷系列答案
相关题目
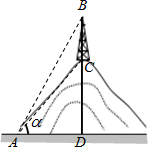课外兴趣小组要在操场上借助侧倾器测量学校对面小山CD的高度．在A处测得山顶电信塔顶B处的仰角∠β=60°，塔脚C处的仰角∠α=45°．已知电信塔高BC=21米，求山高CD．（参考数据：$\sqrt{2}≈1.4，\sqrt{3}≈1.7，\sqrt{5}≈2.2$）
19．下列能判定△ABC为等腰三角形的是（ ）
| A． | ∠A=40°、∠B=50° | B． | ∠A=40°、∠B=70° | ||
| C． | AB=AC=3，BC=6 | D． | AB=3、BC=8，周长为16 |
如图，在△ABC中，AB=AD=DC，∠BAD=40°，则∠DAC=35°．
请根据图中提供的信息，回答下列问题：