题目内容
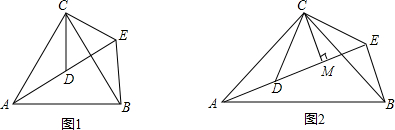
6. 如图,在梯形ABCD中,AD∥BC,S△AOD:S△BOC=1:9.
如图,在梯形ABCD中,AD∥BC,S△AOD:S△BOC=1:9.(1)求AD:BC的值;
(2)若S1=2,求梯形ABCD的面积.
分析 (1)根据相似三角形的判定方法,由AD∥BC可判断△AOD∽△COB,则根据相似三角形的性质得($\frac{AD}{BC}$)2=$\frac{1}{9}$,利用算术平方根的定义易得AD:BC=1:3;
(2)根据相似三角形的性质,由△AOD∽△COB得到$\frac{OD}{OB}$=$\frac{AO}{CO}$=$\frac{AD}{BC}$=$\frac{1}{3}$,则根据三角形面积公式得S2=2S1=4,S4=2S1=4,加上S3=9S1=18,于是计算S1+S2+S3+S4即可.
解答 解:(1)∵AD∥BC,
∴△AOD∽△COB,
∴$\frac{{S}_{△AOD}}{{S}_{△COB}}$=($\frac{AD}{BC}$)2=$\frac{1}{9}$,
∴AD:BC=1:3;
(2)∵△AOD∽△COB,
∴$\frac{OD}{OB}$=$\frac{AO}{CO}$=$\frac{AD}{BC}$=$\frac{1}{3}$,
∴S2=2S1=4,S4=2S1=4,
而S3=9S1=18,
∴梯形ABCD的面积=S1+S2+S3+S4=2+4+18+4=28.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.本题的关键是等高的三角形面积的比等于底边的比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.二次函数y=2x2-4x-1的顶点式是( )
| A. | y=(2x-1)2-2 | B. | y=2(x-1)2-3 | C. | y=2(x+1)2-3 | D. | y=2(x+1)2+3 |
 如图,在正方形网格中,每个小正方形的边长都为1,点A,点B在网格中的位置如图所示.
如图,在正方形网格中,每个小正方形的边长都为1,点A,点B在网格中的位置如图所示.
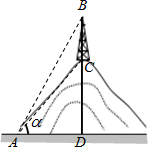 课外兴趣小组要在操场上借助侧倾器测量学校对面小山CD的高度.在A处测得山顶电信塔顶B处的仰角∠β=60°,塔脚C处的仰角∠α=45°.已知电信塔高BC=21米,求山高CD.(参考数据:$\sqrt{2}≈1.4,\sqrt{3}≈1.7,\sqrt{5}≈2.2$)
课外兴趣小组要在操场上借助侧倾器测量学校对面小山CD的高度.在A处测得山顶电信塔顶B处的仰角∠β=60°,塔脚C处的仰角∠α=45°.已知电信塔高BC=21米,求山高CD.(参考数据:$\sqrt{2}≈1.4,\sqrt{3}≈1.7,\sqrt{5}≈2.2$) 如图,在△ABC中,AB=AD=DC,∠BAD=40°,则∠DAC=35°.
如图,在△ABC中,AB=AD=DC,∠BAD=40°,则∠DAC=35°.