题目内容
8．已知，一组数据x1，x2…x9的平均数为5，方差为2，则数据2x1+1，2x2+1…2x9+1的平均数和方差分别为（ ）| A． | 5、4 | B． | 6、2 | C． | 11、4 | D． | 11、8 |
分析 设一组数据x1，x2…x9的平均数为$\overline{x}$=5，方差是s2=2，依此可得另一组数据2x1+1，2x2+1…2x9+1的平均数与方差．
解答 解：设一组数据x1，x2…x9的平均数为$\overline{x}$=5，方差是s2=2，
则另一组数据2x1+1，2x2+1…2x9+1的平均数为$\overline{x′}$=2$\overline{x}$+1=2×5+1=11，方差为s′2=22s2=8，
故选D．
点评 本题考查了方差与平均数，用到的知识点：如果一组数据x1，x2，…，xn的平均数为$\overline{x}$，方差为S2，那么另一组数据ax1+b，ax2+b，…，axn+b的平均数为a$\overline{x}$+b，方差为a2S2．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
相关题目
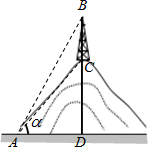课外兴趣小组要在操场上借助侧倾器测量学校对面小山CD的高度．在A处测得山顶电信塔顶B处的仰角∠β=60°，塔脚C处的仰角∠α=45°．已知电信塔高BC=21米，求山高CD．（参考数据：$\sqrt{2}≈1.4，\sqrt{3}≈1.7，\sqrt{5}≈2.2$）
19．下列能判定△ABC为等腰三角形的是（ ）
| A． | ∠A=40°、∠B=50° | B． | ∠A=40°、∠B=70° | ||
| C． | AB=AC=3，BC=6 | D． | AB=3、BC=8，周长为16 |
如图，在△ABC中，AB=AD=DC，∠BAD=40°，则∠DAC=35°．
请根据图中提供的信息，回答下列问题：
18．给出三个不等式：①4+2a＞3+2a；②4-a＞3-a；③4a＞3a（a≠0）．其中正确的是（ ）
| A． | ①② | B． | ③ | C． | ②③ | D． | ①②③ |