题目内容
17.据报道,“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.某校学生会想知道学生对这个提议的了解程度,随机抽取部分学生进行了一次问卷调查,并根据收集到的信息进行了统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题: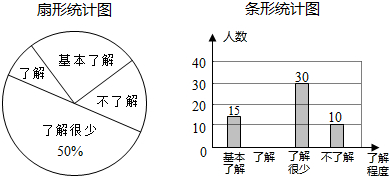
(1)接受问卷调查的学生共有,60名,扇形统计图中“基本了解”部分所对应扇形的圆心角为90°;请补全条形统计图;
(2)若该校共有学生900人,请根据上述调查结果,估计该校学生中对将“剪刀石头布”作为奥运会比赛项目的提议达到“了解”和“基本了解”程度的总人数;
(3)“剪刀石头布”比赛时双方每次任意出“剪刀”、“石头”、“布”这三种手势中的一种,规则为:剪刀胜布,布胜石头,石头胜剪刀,若双方出现相同手势,则算打平.若小刚和小明两人只比赛一局,请用树状图或列表法求两人打平的概率.
分析 (1)由“了解很少”的人数除以占的百分比得出学生总数,求出“基本了解”的学生占的百分比,乘以360得到结果,补全条形统计图即可;
(2)求出“了解”和“基本了解”程度的百分比之和,乘以900即可得到结果;
(3)列表得出所有等可能的情况数,找出两人打平的情况数,即可求出所求的概率.
解答 解:(1)根据题意得:30÷50%=60(名),“了解”人数为60-(15+30+10)=5(名),
“基本了解”占的百分比为$\frac{15}{60}$×100%=25%,占的角度为25%×360°=90°,
故答案为:60,90°;
补全条形统计图如图所示:
(2)根据题意得:900×$\frac{15+5}{60}$=300(人),
则估计该校学生中对将“剪刀石头布”作为奥运会比赛项目的提议达到“了解”和“基本了解”程度的总人数为300人;
(3)列表如下:
| 剪 | 石 | 布 | |
| 剪 | (剪,剪) | (石,剪) | (布,剪) |
| 石 | (剪,石) | (石,石) | (布,石) |
| 布 | (剪,布) | (石,布) | (布,布) |
则P=$\frac{3}{9}=\frac{1}{3}$.
点评 本题考查的是扇形统计图以及用列表法或画树形图法求随机事件的概率,熟知扇形统计图及条形统计图的定义是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.设a=$\sqrt{43}-1$,a在两个相邻整数之间,则这两个整数是( )
| A. | 2和3 | B. | 3和4 | C. | 4和5 | D. | 5和6 |
12.判断$\sqrt{11}×\sqrt{30}$的值会介于下列哪两个整数之间( )
| A. | 17,18 | B. | 18,19 | C. | 19,20 | D. | 21,22 |
7.若一个多边形的内角和等于1620°,则这个多边形的边数为( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
 如图所示的是由一些相同的小正方体组成的简单几何体的主视图和俯视图,设组成这个几何体的小正方体的个数为n,则n的最大值为( )
如图所示的是由一些相同的小正方体组成的简单几何体的主视图和俯视图,设组成这个几何体的小正方体的个数为n,则n的最大值为( )