题目内容
6.(1)解不等式$\frac{x-2}{2}≥\frac{7-x}{3}$,并把它的解集表示在数轴上.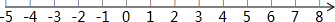
(2)解不等式组$\left\{\begin{array}{l}{3x-3<2x①}\\{\frac{x-1}{2}≤2x+1②}\end{array}\right.$,并把它的解集表示在数轴上.
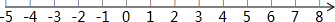
分析 (1)去分母,去括号,移项,合并同类项,系数化成1,最后在数轴上表示出来即可;
(2)先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:(1)$\frac{x-2}{2}≥\frac{7-x}{3}$,
去分母得:3(x-2)≥2(7-x),
3x-6≥14-2x,
3x+2x≥14+6,
5x≥20,
x≥4,
在数轴上表示不等式的解集为: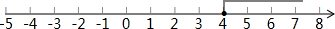 ;
;
(2)$\left\{\begin{array}{l}{3x-3<2x①}\\{\frac{x-1}{2}≤2x+1②}\end{array}\right.$,
∵解不等式①得:x<3,
解不等式②得:x≥-1,
∴不等式组的解集为-1≤x<3,
在数轴上表示不等式组的解集为: .
.
点评 本题考查了解一元一次不等式组和解一元一次不等式,在数轴上表示不等式或不等式组的解集的应用,能求出不等式的解集和能根据不等式的解集找出不等式组的解集是解此题的关键.

练习册系列答案
相关题目
14.若x是81的算术平方根,则x=( )
| A. | 9 | B. | -9 | C. | ±9 | D. | 81 |
15.下列二次根式中,属于最简二次根式的是( )
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\sqrt{5}$ | C. | $\sqrt{4}$ | D. | $\sqrt{0.8}$ |
 如图,已知在长方形ABCD中,AD=10,CD=5,点E从点D出发,沿线段DA以每秒1个单位长的速度向点A方向移动,同时点F从点C出发,沿射线CD方向以每秒2个单位长的速度移动,当B、E、F三点共线时,两点同时停止运动,此时BF⊥CE.设点E移动的时间为t(秒).
如图,已知在长方形ABCD中,AD=10,CD=5,点E从点D出发,沿线段DA以每秒1个单位长的速度向点A方向移动,同时点F从点C出发,沿射线CD方向以每秒2个单位长的速度移动,当B、E、F三点共线时,两点同时停止运动,此时BF⊥CE.设点E移动的时间为t(秒).
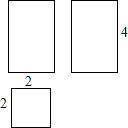 如图,是一个长方体的三视图(单位:cm),这个长方形的体积是16cm3.
如图,是一个长方体的三视图(单位:cm),这个长方形的体积是16cm3.