题目内容
19.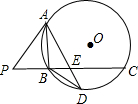 如图,已知PA是⊙O的切线,切点为A,PC与⊙O相交于B,C点,且AB⊥PC于点B,点D为$\widehat{BC}$上一点,连接AD于点E,且∠PAB=∠DAB.
如图,已知PA是⊙O的切线,切点为A,PC与⊙O相交于B,C点,且AB⊥PC于点B,点D为$\widehat{BC}$上一点,连接AD于点E,且∠PAB=∠DAB.(1)求证:AB=BD;
(2)若AB=8,tan∠P=$\frac{4}{3}$,求⊙O的半径.
分析 (1)由弦切角定理得出∠PAB=∠D,由∠PAB=∠DAB,得出∠D=∠DAB,即可得出结论;
(2)连接AC,先证明AC是⊙O的直径,再由三角函数求出PB,由勾股定理求出PA,证明△PAC∽△PBA,得出对应边成比例求出AC,即可得出⊙O的半径.
解答 (1)证明:∵PA是⊙O的切线,
∴∠PAB=∠D,
∵∠PAB=∠DAB,
∴∠D=∠DAB,
∴AB=BD;
(2)解:连接AC,如图所示: ∵AB⊥PC,
∵AB⊥PC,
∴∠ABP=∠ABC=90°,
∴AC是⊙O的直径,
∵AB=8,tan∠P=$\frac{AB}{PB}$=$\frac{4}{3}$,
∴PB=6,
∴PA=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵PA是⊙O的切线,
∴∠PAC=90°,
∴∠PAC=∠ABP=90°,
又∵∠P=∠P,
∴△PAC∽△PBA,
∴$\frac{AC}{AB}=\frac{PA}{PB}$,
即$\frac{AC}{8}=\frac{10}{6}$,
解得:AC=$\frac{40}{3}$,
∴OA=$\frac{1}{2}$AC=$\frac{20}{3}$,
即⊙O的半径为$\frac{20}{3}$.
点评 本题考查了切线的性质、弦切角定理、三角函数、勾股定理、相似三角形的判定与性质;熟练掌握切线的性质和圆的有关定理,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.若有一个n边形,其内角和大于它的外角和,则n的值至少为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
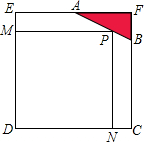 已知边长为4的正方形截取一个角后成为五边形ABCDE(如图),其中AF=2,BF=1.若在AB上有一点P使矩形MPND的面积最大,请你求出此时矩形MPND的边长DN、PN.
已知边长为4的正方形截取一个角后成为五边形ABCDE(如图),其中AF=2,BF=1.若在AB上有一点P使矩形MPND的面积最大,请你求出此时矩形MPND的边长DN、PN. 如图,C是以AB为直径的⊙O上一点,过O作OE⊥AC于点E,过点A作⊙O的切线交OE的延长线于点F,连接CF并延长交BA的延长线于点P.
如图,C是以AB为直径的⊙O上一点,过O作OE⊥AC于点E,过点A作⊙O的切线交OE的延长线于点F,连接CF并延长交BA的延长线于点P.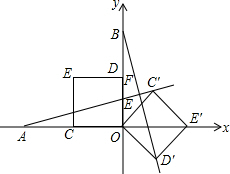 如图,在平面直角坐标系中,O为原点,点A的坐标为(-4,0),点B的坐标为(0,4),点C、D分别为OA、OB的中点,若正方形OCED绕点O顺时针旋转,得正方形OC′E′D′.记旋转角为a(0°<a<360°),连结AC′、BD′,设直线AC′与直线BD′相交于点F,则点F的纵坐标的最大值为$\sqrt{3}$+1.
如图,在平面直角坐标系中,O为原点,点A的坐标为(-4,0),点B的坐标为(0,4),点C、D分别为OA、OB的中点,若正方形OCED绕点O顺时针旋转,得正方形OC′E′D′.记旋转角为a(0°<a<360°),连结AC′、BD′,设直线AC′与直线BD′相交于点F,则点F的纵坐标的最大值为$\sqrt{3}$+1.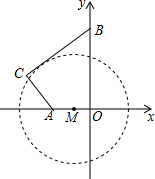 某地质公园为了方便游客,计划修建一条栈道BC连接两条进入观景台OA的栈道AC和OB,其中AC⊥BC,同时为减少对地质地貌的破坏,设立一个圆形保护区⊙M(如图所示),M是OA上一点,⊙M与BC相切,观景台的两端A、O到⊙M上任意一点的距离均不小于80米.经测量,OA=60米,OB=170米,tan∠OBC=$\frac{4}{3}$.
某地质公园为了方便游客,计划修建一条栈道BC连接两条进入观景台OA的栈道AC和OB,其中AC⊥BC,同时为减少对地质地貌的破坏,设立一个圆形保护区⊙M(如图所示),M是OA上一点,⊙M与BC相切,观景台的两端A、O到⊙M上任意一点的距离均不小于80米.经测量,OA=60米,OB=170米,tan∠OBC=$\frac{4}{3}$.