题目内容
4. 如图,C是以AB为直径的⊙O上一点,过O作OE⊥AC于点E,过点A作⊙O的切线交OE的延长线于点F,连接CF并延长交BA的延长线于点P.
如图,C是以AB为直径的⊙O上一点,过O作OE⊥AC于点E,过点A作⊙O的切线交OE的延长线于点F,连接CF并延长交BA的延长线于点P.(1)求证:PC是⊙O的切线;
(2)若AB=4,AP:PC=1:2,求CF的长.
分析 (1)连接OC,证明△AOF≌△COF,得到∠OCF=∠OAF=90°,根据切线的判定定理证明PC是⊙O的切线;
(2)根据切线长定理求出PC的长,根据平行线分线段成比例定理得到PF与FC之比,计算得到答案.
解答  (1)证明:连接OC,
(1)证明:连接OC,
∵AB为⊙O的直径,∠ACB=90°,又OE⊥AC,
∴BC∥OF,
∴∠AOF=∠OBC,∠FOC=∠OCB,
∵OB=OC,∴∠OBC=∠OCB,
∴∠AOF=∠COF,
在△AOF和△COF中,
$\left\{\begin{array}{l}{OA=OC}\\{∠AOF=∠COF}\\{OF=OF}\end{array}\right.$,
∴△AOF≌△COF,
∴∠OCF=∠OAF=90°,
∴PC是⊙O的切线;
(2)设AP=x,则PC=2x,
由切割线定理得,PC2=PA•PB,
即4x2=x(x+4),
解得x=$\frac{4}{3}$,
∵BC∥OF,∴$\frac{PF}{FC}$=$\frac{PO}{OB}$,
解得,FC=$\frac{1}{2}$.
点评 本题考查的是切线的判定和性质、全等三角形的判定和性质,掌握相关的判定定理和性质定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.从1至9这些数字中任意取一个,取出的数字是奇数的概率是( )
| A. | 0 | B. | 1 | C. | $\frac{5}{9}$ | D. | $\frac{4}{9}$ |
9. 如图,用宽度都是2的矩形纸带叠放成一个锐角为60°的四边形,则此四边形的面积S为( )
如图,用宽度都是2的矩形纸带叠放成一个锐角为60°的四边形,则此四边形的面积S为( )
 如图,用宽度都是2的矩形纸带叠放成一个锐角为60°的四边形,则此四边形的面积S为( )
如图,用宽度都是2的矩形纸带叠放成一个锐角为60°的四边形,则此四边形的面积S为( )| A. | 4 | B. | $\frac{4}{3}$$\sqrt{3}$ | C. | $\frac{2}{3}$$\sqrt{3}$ | D. | $\frac{8}{3}$$\sqrt{3}$ |
16.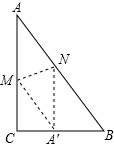 如图,直角三角形纸片ABC中,∠ABC=90°,AC=4,BC=3,折叠纸片,使顶点A落在直角边BC上的点A′处,折痕MN分别交AC、AB于M、N,若NA′⊥BC,则A′B的长为( )
如图,直角三角形纸片ABC中,∠ABC=90°,AC=4,BC=3,折叠纸片,使顶点A落在直角边BC上的点A′处,折痕MN分别交AC、AB于M、N,若NA′⊥BC,则A′B的长为( )
 如图,直角三角形纸片ABC中,∠ABC=90°,AC=4,BC=3,折叠纸片,使顶点A落在直角边BC上的点A′处,折痕MN分别交AC、AB于M、N,若NA′⊥BC,则A′B的长为( )
如图,直角三角形纸片ABC中,∠ABC=90°,AC=4,BC=3,折叠纸片,使顶点A落在直角边BC上的点A′处,折痕MN分别交AC、AB于M、N,若NA′⊥BC,则A′B的长为( )| A. | $\frac{5}{4}$ | B. | $\frac{5}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
 如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,若EC=3,则EF的长为6.
如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,若EC=3,则EF的长为6.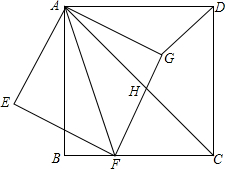 如图,正方形ABCD中,点F是BC边上一点,连结AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连结DG.
如图,正方形ABCD中,点F是BC边上一点,连结AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连结DG.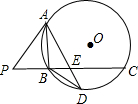 如图,已知PA是⊙O的切线,切点为A,PC与⊙O相交于B,C点,且AB⊥PC于点B,点D为$\widehat{BC}$上一点,连接AD于点E,且∠PAB=∠DAB.
如图,已知PA是⊙O的切线,切点为A,PC与⊙O相交于B,C点,且AB⊥PC于点B,点D为$\widehat{BC}$上一点,连接AD于点E,且∠PAB=∠DAB. 已知,点E是AB的中点,AF=BD,BD=5,AC=7,求DC.
已知,点E是AB的中点,AF=BD,BD=5,AC=7,求DC.