题目内容
11.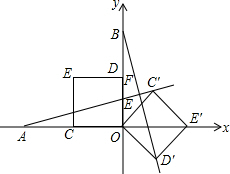 如图,在平面直角坐标系中,O为原点,点A的坐标为(-4,0),点B的坐标为(0,4),点C、D分别为OA、OB的中点,若正方形OCED绕点O顺时针旋转,得正方形OC′E′D′.记旋转角为a(0°<a<360°),连结AC′、BD′,设直线AC′与直线BD′相交于点F,则点F的纵坐标的最大值为$\sqrt{3}$+1.
如图,在平面直角坐标系中,O为原点,点A的坐标为(-4,0),点B的坐标为(0,4),点C、D分别为OA、OB的中点,若正方形OCED绕点O顺时针旋转,得正方形OC′E′D′.记旋转角为a(0°<a<360°),连结AC′、BD′,设直线AC′与直线BD′相交于点F,则点F的纵坐标的最大值为$\sqrt{3}$+1.
分析 首先找到使点F的纵坐标最大时点F的位置(点F与点E′重合时),然后运用勾股定理及30°角所对的直角边等于斜边的一半等知识即可求出点F的纵坐标的最大值.
解答 解:如图,
∵∠AOB=∠D′OC′,
∴∠ACO′=∠BOD′,
在△AOC′和△BOD′中,
$\left\{\begin{array}{l}{AO=BO}\\{∠AOC′=∠BOD′}\\{OC′=OD′}\end{array}\right.$,
∴△AOC′≌△BOD′,
∴∠OAF=∠OBF,
∵∠AGO=∠BOF
∴∠BFA=∠BOA=90°,
∴点F、B、A、O四点共圆,
∴当点F在劣弧上运动时,点F的纵坐标随∠FAO的增大而增大,
∵OC′=2,
∴点C′在以点O为圆心,2为半径的圆O上运动,
∴当AF与⊙O相切时,∠C′AO(即∠FAO)最大,
此时∠AC′O=90°,点E′与点F重合,点F的纵坐标达到最大.
过点F作FH⊥x轴,垂足为H,如图所示.
∵∠AC′O=90°,C′O=2,AO=4,
∴∠E′AO=30°,AC′=2$\sqrt{3}$.
∴AF=2$\sqrt{3}$+2.
∵∠AHF=90°,∠FAH=30°,
∴FH=$\frac{1}{2}$AF=$\frac{1}{2}$×(2$\sqrt{3}$+2)=$\sqrt{3}$+1.
∴点P的纵坐标的最大值为$\sqrt{3}$+1.
点评 本题主要考查了几何变换综合题,涉及全等三角形的判定与性质、勾股定理、三角形的外角性质、30°角所对的直角边等于斜边的一半等知识,找到使点F的纵坐标最大时点F的位置是解决问题的关键.

练习册系列答案
相关题目
16.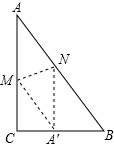 如图,直角三角形纸片ABC中,∠ABC=90°,AC=4,BC=3,折叠纸片,使顶点A落在直角边BC上的点A′处,折痕MN分别交AC、AB于M、N,若NA′⊥BC,则A′B的长为( )
如图,直角三角形纸片ABC中,∠ABC=90°,AC=4,BC=3,折叠纸片,使顶点A落在直角边BC上的点A′处,折痕MN分别交AC、AB于M、N,若NA′⊥BC,则A′B的长为( )
 如图,直角三角形纸片ABC中,∠ABC=90°,AC=4,BC=3,折叠纸片,使顶点A落在直角边BC上的点A′处,折痕MN分别交AC、AB于M、N,若NA′⊥BC,则A′B的长为( )
如图,直角三角形纸片ABC中,∠ABC=90°,AC=4,BC=3,折叠纸片,使顶点A落在直角边BC上的点A′处,折痕MN分别交AC、AB于M、N,若NA′⊥BC,则A′B的长为( )| A. | $\frac{5}{4}$ | B. | $\frac{5}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
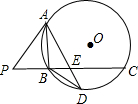 如图,已知PA是⊙O的切线,切点为A,PC与⊙O相交于B,C点,且AB⊥PC于点B,点D为$\widehat{BC}$上一点,连接AD于点E,且∠PAB=∠DAB.
如图,已知PA是⊙O的切线,切点为A,PC与⊙O相交于B,C点,且AB⊥PC于点B,点D为$\widehat{BC}$上一点,连接AD于点E,且∠PAB=∠DAB. 如图,将平行四边形ABCD折叠,使点A与C重合,折痕为EF.若∠A=60,AD=4,AB=6,则AE为$\frac{19}{4}$.
如图,将平行四边形ABCD折叠,使点A与C重合,折痕为EF.若∠A=60,AD=4,AB=6,则AE为$\frac{19}{4}$.