题目内容
4.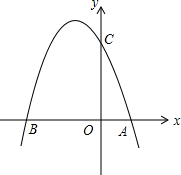 如图,抛物线y=-x2-2x+3与y轴交于点C,与x轴交于点A、B(点B在点A的左侧),设J为y轴正半轴上的一个点,请在抛物线y=-x2-2x+3上求一点K,使得△OKJ为等腰直角三角形.
如图,抛物线y=-x2-2x+3与y轴交于点C,与x轴交于点A、B(点B在点A的左侧),设J为y轴正半轴上的一个点,请在抛物线y=-x2-2x+3上求一点K,使得△OKJ为等腰直角三角形.
分析 分∠OKJ=90°及∠KOJ=90°两种情况考虑,当∠OKJ=90°时,根据等腰直角三角形的性质可以设点J的坐标为(0,2n)(n>0),用n表示出来K点的坐标,将K点的坐标代入抛物线解析式中得到关于n的一元二次方程,解方程即可得出n值,由此得出K点的坐标;当∠KOJ=90°时,点K与点A(或点B)重合,利用二次函数图象上点的坐标特征即可求出点A、B的坐标,从而得出点K的坐标.综上此题得解.
解答 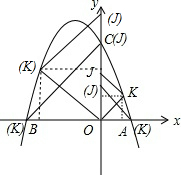 解:当∠OKJ=90°时,
解:当∠OKJ=90°时,
设J点的坐标为(0,2n)(n>0).
∵△OKJ为等腰直角三角形,
∴K点的坐标为(-n,n)或(n,n).
∵点K为抛物线图象上的点,
∴有n=-n2+2n+3,或n=-n2-2n+3,
解得:n1=$\frac{1+\sqrt{13}}{2}$,n2=$\frac{1-\sqrt{13}}{2}$(舍去);或n1=$\frac{\sqrt{21}-3}{2}$,n2=$\frac{-\sqrt{21}-3}{2}$(舍去);
当∠KOJ=90°时,点K与点A(或点B)重合,
∵y=-x2-2x+3=-(x+3)(x-1)=0,
∴点B(-3,0),点A(1,0),
∴此时点K为(-3,0)或(1,0).
故点K的坐标为(-$\frac{1+\sqrt{13}}{2}$,$\frac{1+\sqrt{13}}{2}$)或($\frac{\sqrt{21}-3}{2}$,$\frac{\sqrt{21}-3}{2}$)或(-3,0)或(1,0).
点评 本题考查了等腰直角三角形的性质、抛物线与x轴的交点以及解一元二次方程,分∠OKJ=90°及∠KOJ=90°两种情况考虑是解题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
12.多项式5mx3+25mx2-10mxy各项的公因式是( )
| A. | 5mx2 | B. | 5mxy | C. | mx | D. | 5mx |
16.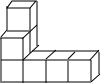 如图,是由相同小正方形组成的立方体图形,它的左视图为( )
如图,是由相同小正方形组成的立方体图形,它的左视图为( )
 如图,是由相同小正方形组成的立方体图形,它的左视图为( )
如图,是由相同小正方形组成的立方体图形,它的左视图为( )| A. | 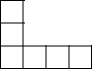 | B. | 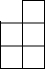 | C. | 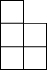 | D. |  |
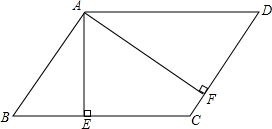 如图.在平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为点E,F.该图中与∠EAF相等的有∠B、∠D.
如图.在平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为点E,F.该图中与∠EAF相等的有∠B、∠D. 如图,在?ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=54°,则∠BCE的度数为36°.
如图,在?ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=54°,则∠BCE的度数为36°.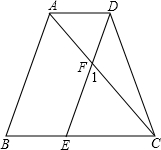 如图,已知AD∥BC,∠1=∠ACB,AC平分∠DAB,试说明:AB∥DE.
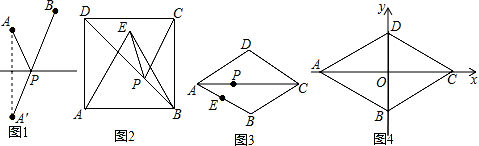
如图,已知AD∥BC,∠1=∠ACB,AC平分∠DAB,试说明:AB∥DE. 如图,在Rt△ABC中,∠C=90°,AC=1,BC=$\sqrt{3}$,点O为Rt△ABC内一点,连接A0、BO、CO,且∠AOC=∠COB=BOA=120°,按下列要求画图(保留画图痕迹):以点B为旋转中心,将△AOB绕点B顺时针方向旋转60°,得到△A′O′B(得到A、O的对应点分别为点A′、O′),则∠A′BC=90°,OA+OB+OC=$\sqrt{7}$.
如图,在Rt△ABC中,∠C=90°,AC=1,BC=$\sqrt{3}$,点O为Rt△ABC内一点,连接A0、BO、CO,且∠AOC=∠COB=BOA=120°,按下列要求画图(保留画图痕迹):以点B为旋转中心,将△AOB绕点B顺时针方向旋转60°,得到△A′O′B(得到A、O的对应点分别为点A′、O′),则∠A′BC=90°,OA+OB+OC=$\sqrt{7}$.