题目内容
15．
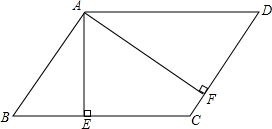如图．在平行四边形ABCD中，AE⊥BC，AF⊥CD，垂足分别为点E，F．该图中与∠EAF相等的有∠B、∠D．
分析 四边形AECF中利用四边形的内角和定理得到∠C+∠AEF=180°，然后根据平行线的性质可得∠C+∠D=180°，得到∠AEF=∠D，然后根据平行四边形的对角相等求解．
解答 解：∵AE⊥BC，AF⊥CD，
∴∠AEC=∠AFC=90°，
∴四边形AECF中，∠C+∠AEF=180°，
又∵平行四边形ABCD中，AD∥BC，
∴∠C+∠D=180°，
∴∠AEF=∠D，
又∵平行四边形ABCD中，∠B=∠D，
∴∠B=∠D=∠AEF．
故答案是：∠B、∠D．
点评 本题考查了平行四边形的性质：平行四边形的对边平行，对角相等，理解性质是关键．
练习册系列答案
相关题目
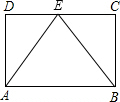如图，平行四边形ABCD中，E是CD的中点，△ABE是等边三角形．求证：四边形ABCD是矩形．
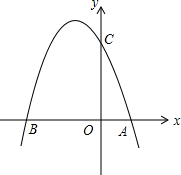如图，抛物线y=-x2-2x+3与y轴交于点C，与x轴交于点A、B（点B在点A的左侧），设J为y轴正半轴上的一个点，请在抛物线y=-x2-2x+3上求一点K，使得△OKJ为等腰直角三角形．
