题目内容
19.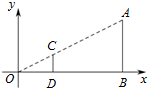 如图,点A(6,3)、B(6,0)在直角坐标系内.以原点O为位似中心,相似比为$\frac{1}{3}$,在第一象限内把线段AB缩小后得到线段CD,那么点C的坐标为( )
如图,点A(6,3)、B(6,0)在直角坐标系内.以原点O为位似中心,相似比为$\frac{1}{3}$,在第一象限内把线段AB缩小后得到线段CD,那么点C的坐标为( )| A. | (3,1) | B. | (2,0) | C. | (3,3) | D. | (2,1) |
分析 根据得A、B的坐标求出OB、AB的长,根据位似的概念得到比例式,计算求出OD、CD的长,得到点C的坐标.
解答 解:∵A(6,3)、B(6,0),
∴OB=6,AB=3,
由题意得,△ODC∽△OBA,相似比为$\frac{1}{3}$,
∴$\frac{OD}{OB}$=$\frac{CD}{AB}$=$\frac{1}{3}$,
∴OD=2,CD=1,
∴点C的坐标为(2,1),
故选:D.
点评 本题考查的是位似变换的概念和性质以及坐标与图形的性质,掌握位似的两个图形一定是相似形和相似三角形的性质是解题的关键.

练习册系列答案
相关题目
4.下列命题是假命题的是( )
| A. | 如果a∥b,b∥c,那么a∥c | |
| B. | 直角三角形的两个锐角互余 | |
| C. | 两条直线被第三条直线所截,内错角相等 | |
| D. | 两点之间,线段最短 |
8.李明去参加聚会,每两人都互相赠送礼物,他发现共送礼物20件,若设有n人参加聚会,根据题意可列出方程为( )
| A. | $\frac{n(n+1)}{2}$=20 | B. | n(n-1)=20 | C. | $\frac{n(n-1)}{2}$=20 | D. | n(n+1)=20 |
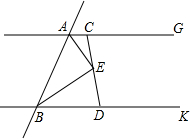 如图,直线AG∥BK,AE、BE分别平分∠GAB、∠KBA,过点E的直线分别交直线AG、BK于C、D点.
如图,直线AG∥BK,AE、BE分别平分∠GAB、∠KBA,过点E的直线分别交直线AG、BK于C、D点. 如图,将一副三角板的直角顶点重合,摆放在桌面上,若∠BOC=63°,则∠AOD=117°.
如图,将一副三角板的直角顶点重合,摆放在桌面上,若∠BOC=63°,则∠AOD=117°.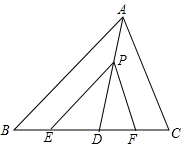 如图,在△ABC中,点D,E,F在边BC上,点P在线段AD上,若PE∥AB,∠PFD=∠C,点D到PE和PF的距离相等.求证:点D到AB和AC的距离相等.
如图,在△ABC中,点D,E,F在边BC上,点P在线段AD上,若PE∥AB,∠PFD=∠C,点D到PE和PF的距离相等.求证:点D到AB和AC的距离相等.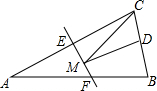 如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )
如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )