题目内容
9.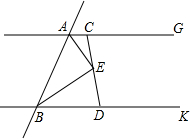 如图,直线AG∥BK,AE、BE分别平分∠GAB、∠KBA,过点E的直线分别交直线AG、BK于C、D点.
如图,直线AG∥BK,AE、BE分别平分∠GAB、∠KBA,过点E的直线分别交直线AG、BK于C、D点.(1)求证:BE⊥AE;
(2)请猜想:AB、AC、BD的数量关系,并证明你的猜想.
分析 (1)根据角平分线的性质和平行线的性质,可以得到∠BAE和∠ABE之间的关系,从而得到∠AEB的度数,从而可以证得结论;
(2)作辅助线在AB上截取AF=AC,画出相应的图形,然后根据题目中的信息,可以得到△EFB和△EDB的关系,从而可以得到BF和BD的关系,进而得到AB与AC、BD的关系.
解答 (1)证明:∵AG∥BK,
∴∠CAB+∠ABD=180°,
∵AE、BE分别平分∠GAB、∠KBA,
∴∠CAE=∠EAB=$\frac{1}{2}$∠CAB,∠ABE=∠EBD=$\frac{1}{2}$∠ABD,
∴∠EAB+∠ABE=90°,
∴∠AEB=90°,
即BE⊥AE;
(2)AB、AC、BD的数量关系是:AB=AC+BD;理由:
证明:在AB上截取AF=AC,如下如所示:
∵AE、BE分别平分∠GAB、∠KBA,
∴∠CAE=∠EAB=$\frac{1}{2}$∠CAB,∠ABE=∠EBD=$\frac{1}{2}$∠ABD,
在△CAE和△FAE中,
$\left\{\begin{array}{l}{AE=AE}\\{∠CAE=∠FAE}\\{AC=AF}\end{array}\right.$,
∴△CAE≌△FAE(SAS)
∴∠CEA=∠FEA,
∵∠CEA+∠FEA+∠FEB+∠DFB=360°,BE⊥AE,
∴∠AEF+∠FEB=90°,∠CEA+∠DEB=90°,
∴∠FEB=∠DEB,
在△EFB和△EDB中,
$\left\{\begin{array}{l}{∠FBE=∠DBE}\\{BE=BE}\\{∠FEB=∠DEB}\end{array}\right.$,
∴△EFB≌△EDB(ASA),
∴BF=BD,
∵AC=AF,AB=AF+BF,
∴AB=AC+BD,
即AB、AC、BD的数量关系是:AB=AC+BD.
点评 本题考查全等三角形的判定与性质、角平分线的性质、角平分线的性质,解题的关键是明确题意找出所求问题需要的条件.

| 名称 | 三棱柱 | 四棱柱 | 五棱柱 | 六棱柱 |
| 图形 | 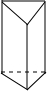 | 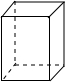 | 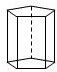 |  |
| 顶点数a | 6 | 8 | 10 | 12 |
| 棱数b | 9 | 12 | 15 | 18 |
| 面数c | 5 | 6 | 7 | 8 |
(2)若某个棱柱由30个面构成,则这个棱柱为二十八棱柱;
(3)若一个棱柱的底面多边形的边数为n,则它有n个侧面,共有n+2个面,共有2n个顶点,共有3n条棱;
(4)观察表中的结果,你能发现a,b,c之间有什么关系吗?请写出关系式.
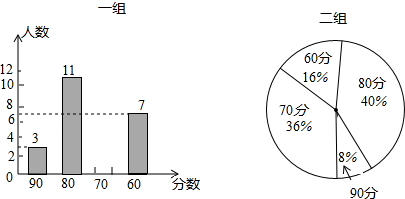
请你根据以上提供的信息解答下列问题:
(1)请你将表格补充完整:
| 平均数 | 中位数 | 众数 | 方差 | |
| 一组 | 74 | 80 | 80 | 104 |
| 二组 | 74 | 70 | 80 | 72 |
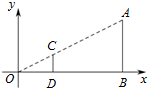 如图,点A(6,3)、B(6,0)在直角坐标系内.以原点O为位似中心,相似比为$\frac{1}{3}$,在第一象限内把线段AB缩小后得到线段CD,那么点C的坐标为( )
如图,点A(6,3)、B(6,0)在直角坐标系内.以原点O为位似中心,相似比为$\frac{1}{3}$,在第一象限内把线段AB缩小后得到线段CD,那么点C的坐标为( )| A. | (3,1) | B. | (2,0) | C. | (3,3) | D. | (2,1) |
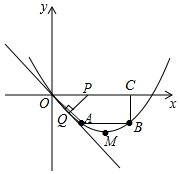 已知,如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(1,-1),B(3,-1),动点P从点O出发,沿着x轴正方向以每秒2个单位长度的速度移动,过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2),△OPQ与四边形OABC重叠部分的面积为S.
已知,如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(1,-1),B(3,-1),动点P从点O出发,沿着x轴正方向以每秒2个单位长度的速度移动,过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2),△OPQ与四边形OABC重叠部分的面积为S.