题目内容
9.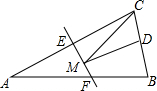 如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )
如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
分析 连接AD,由于△ABC是等腰三角形,点D是BC边的中点,故AD⊥BC,再根据三角形的面积公式求出AD的长,再再根据EF是线段AC的垂直平分线可知,点C关于直线EF的对称点为点A,故AD的长为CM+MD的最小值,由此即可得出结论.
解答 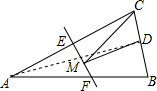 解:连接AD,
解:连接AD,
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×4×AD=16,解得AD=8,
∵EF是线段AC的垂直平分线,
∴点C关于直线EF的对称点为点A,
∴AD的长为CM+MD的最小值,
∴△CDM的周长最短=(CM+MD)+CD=AD+$\frac{1}{2}$BC=8+$\frac{1}{2}$×4=8+2=10.
故选C.
点评 本题考查的是轴对称-最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
19.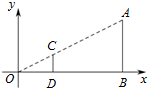 如图,点A(6,3)、B(6,0)在直角坐标系内.以原点O为位似中心,相似比为$\frac{1}{3}$,在第一象限内把线段AB缩小后得到线段CD,那么点C的坐标为( )
如图,点A(6,3)、B(6,0)在直角坐标系内.以原点O为位似中心,相似比为$\frac{1}{3}$,在第一象限内把线段AB缩小后得到线段CD,那么点C的坐标为( )
 如图,点A(6,3)、B(6,0)在直角坐标系内.以原点O为位似中心,相似比为$\frac{1}{3}$,在第一象限内把线段AB缩小后得到线段CD,那么点C的坐标为( )
如图,点A(6,3)、B(6,0)在直角坐标系内.以原点O为位似中心,相似比为$\frac{1}{3}$,在第一象限内把线段AB缩小后得到线段CD,那么点C的坐标为( )| A. | (3,1) | B. | (2,0) | C. | (3,3) | D. | (2,1) |
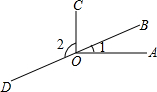 如图,∠1=20°,∠AOC=90°,点B,O,D在同一直线上,则∠2=110°.
如图,∠1=20°,∠AOC=90°,点B,O,D在同一直线上,则∠2=110°.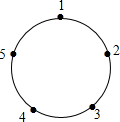 如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下列沿顺时针方向跳两个点:若停在偶数点上,则下次沿逆时针方向跳一个点,若青蛙从1这点开始跳,则经过2016次后它停在哪个数对应的点上( )
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下列沿顺时针方向跳两个点:若停在偶数点上,则下次沿逆时针方向跳一个点,若青蛙从1这点开始跳,则经过2016次后它停在哪个数对应的点上( )