题目内容
6.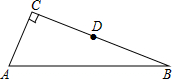 如图,在△ABC中,∠C=90°,AC=5,BC=12,D是BC边的中点.
如图,在△ABC中,∠C=90°,AC=5,BC=12,D是BC边的中点.(1)尺规作图:过点D作DE⊥AB于点E;(保留作图痕迹,不写做法)
(2)求DE的长.
分析 (1)以点D为圆心作一段弧交AB于两点,以这两点为圆心,分别作圆弧交于一点,将D与该点连接即可求作出E.
(2)由勾股定理可求出AB=13,又易证△ACB∽△DEB,从而可知$\frac{DE}{DB}=\frac{AC}{AB}$,化简即可求出DE的长度.
解答 解:(1)如图所示:
(2)∵点D为BC中点,
∴DB=$\frac{1}{2}$BC=$\frac{1}{2}$×12=6,
又∵在Rt△ACB中,∠C=90°,AC=5,BC=12,
∴AB=13,
又∵∠C=∠DEB=90°,∠B=∠B,
∴△ACB∽△DEB,
∴$\frac{DE}{DB}=\frac{AC}{AB}$,
∴$\frac{DE}{6}=\frac{5}{13}$
即DE=$\frac{30}{13}$
点评 本题考查相似三角形的判定与性质,涉及尺规作图,相似三角形的性质与判定,勾股定理,属于中等题型.

练习册系列答案
相关题目
1.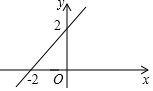 一次函数y=kx+b(k,b是常数,k≠0)的图象如图所示,则不等式kx+b>0的解集是( )
一次函数y=kx+b(k,b是常数,k≠0)的图象如图所示,则不等式kx+b>0的解集是( )
 一次函数y=kx+b(k,b是常数,k≠0)的图象如图所示,则不等式kx+b>0的解集是( )
一次函数y=kx+b(k,b是常数,k≠0)的图象如图所示,则不等式kx+b>0的解集是( )| A. | x>-2 | B. | x>0 | C. | x<-2 | D. | x<0 |
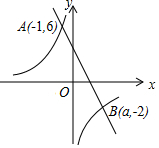 如图,在直角坐标系xoy中,一次函数y1=k1x+b的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(-1,6)、B(a,-2)两点.
如图,在直角坐标系xoy中,一次函数y1=k1x+b的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(-1,6)、B(a,-2)两点.
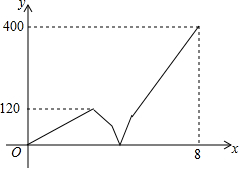 一条笔直的公路上顺次有A、B、C三地,甲车从B地出发往A地匀速行驶,到达A地后停止,在甲车出发的同时,乙车从B地出发往A地匀速行驶,到达A地停留1小时后,调头按原速向C地行驶,若AB两地相距300千米,在两车行驶的过程中,甲、乙两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示,则在他们出发后经过4$\frac{3}{8}$小时相遇.
一条笔直的公路上顺次有A、B、C三地,甲车从B地出发往A地匀速行驶,到达A地后停止,在甲车出发的同时,乙车从B地出发往A地匀速行驶,到达A地停留1小时后,调头按原速向C地行驶,若AB两地相距300千米,在两车行驶的过程中,甲、乙两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示,则在他们出发后经过4$\frac{3}{8}$小时相遇. 如图,已知矩形ABCD.
如图,已知矩形ABCD.