题目内容
15. 如图,已知矩形ABCD.
如图,已知矩形ABCD.(1)尺规作图:按下列要求完成作图(保留作图痕迹,请标明字母)
①作对角线BD的垂直平分线l,交AD、BC于点M、N,与BD相交于点O;
②连接BM、DN.
(2)判断四边形BMDN的形状,并说明理由.
(3)若AB=4,AD=8,求MD的长.
分析 (1)根据垂直平分线的作法画出图形即可;
(2)根据矩形性质求出AD∥BC,推出∠MDO=∠NBO,∠DMO=∠BNO,证△DMO≌△BNO,推出OM=ON,得出平行四边形BMDN,推出菱形BMDN;
(3)根据菱形性质求出DM=BM,在Rt△AMB中,根据勾股定理得出BM2=AM2+AB2,即可列方程求得.
解答  解:(1)如图所示:
解:(1)如图所示:
(2)四边形BMDN是菱形,理由如下:
∵四边形ABCD是矩形
∴AD∥BC,∠A=90°,
∴∠MDO=∠NBO,∠DMO=∠BNO,
∵在△DMO和△BNO中,$\left\{\begin{array}{l}{∠MDO=∠NBO}&{\;}\\{BO=DO}&{\;}\\{∠MOD=∠NOB}&{\;}\end{array}\right.$,
∴△DMO≌△BNO(ASA),
∴OM=ON,
∵OB=OD,
∴四边形BMDN是平行四边形,
∵MN⊥BD,
∴四边形BMDN是菱形.
(3)∵四边形BMDN是菱形,
∴MB=MD,
设MD长为x,则MB=DM=x,
在Rt△AMB中,BM2=AM2+AB2
即x2=(8-x)2+42,
解得:x=5,
即MD长为5.
点评 本题是四边形综合题目,考查了矩形性质,平行四边形的判定,菱形的判定和性质,勾股定理等知识点的应用,对角线互相平分的四边形是平行四边形,对角线互相垂直的平行四边形是菱形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
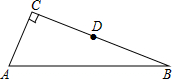 如图,在△ABC中,∠C=90°,AC=5,BC=12,D是BC边的中点.
如图,在△ABC中,∠C=90°,AC=5,BC=12,D是BC边的中点. 如图是由5个相同大小的正方体搭成的几何体,则它的俯视图是( )
如图是由5个相同大小的正方体搭成的几何体,则它的俯视图是( )



 如图,每个小方格都是边长为1的小正方形.
如图,每个小方格都是边长为1的小正方形.