题目内容
9. 如图所示,CP是△ACB的角平分线,O是CP上任意一点,⊙O与AC相切于点E.求证:BC是⊙O的切线.
如图所示,CP是△ACB的角平分线,O是CP上任意一点,⊙O与AC相切于点E.求证:BC是⊙O的切线.
分析 过点O作OF⊥BC,垂足为F,连接OE,根据角平分线的性质可得出OF=OE,继而得出结论.
解答 证明:过点O作OF⊥BC,垂足为F,连接OE,如图所示:
∵⊙O与AC相切于点E,
∴OE⊥AC,
又∵OC为∠ACB的平分线,
∴OF=OE,
即OF是⊙O的半径,
∴BC是⊙O的切线.
点评 本题考查了切线的判定方法、角平分线的性质定理;熟练掌握切线的判定方法,通过作辅助线证明OF=OE是解决问题的关键.

练习册系列答案
相关题目
18.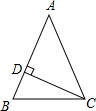 如图,等腰三角形ABC中,AB=AC,∠A=50°,CD⊥AB于D,则∠DCB等于( )
如图,等腰三角形ABC中,AB=AC,∠A=50°,CD⊥AB于D,则∠DCB等于( )
 如图,等腰三角形ABC中,AB=AC,∠A=50°,CD⊥AB于D,则∠DCB等于( )
如图,等腰三角形ABC中,AB=AC,∠A=50°,CD⊥AB于D,则∠DCB等于( )| A. | 40° | B. | 30° | C. | 23° | D. | 25° |
7.三角形的外心具有的性质是( )
| A. | 到三边的距离相等 | B. | 外心一定在三角形外 | ||
| C. | 到三个顶点的距离相等 | D. | 外心一定在三角形内 |
 如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为2m,梯子的顶端B到地面的距离为7m,现将梯子的底端A向外移动到A′,使梯子底端A′到墙根O的距离等于3m,同时梯子的顶端B下降到B′,那么BB′=7-2$\sqrt{11}$m.
如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为2m,梯子的顶端B到地面的距离为7m,现将梯子的底端A向外移动到A′,使梯子底端A′到墙根O的距离等于3m,同时梯子的顶端B下降到B′,那么BB′=7-2$\sqrt{11}$m. 如图,过⊙O上一点C作弦BA的垂线,交BA延长线于D点,连OA、CA,若AC平分∠OAD.
如图,过⊙O上一点C作弦BA的垂线,交BA延长线于D点,连OA、CA,若AC平分∠OAD.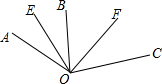 如图所示,若∠AOC=α,过点O点作射线OB,OE平分∠AOB,OF平分∠COB,若∠AOC=(5m+20)°,∠EOF=(m+40)°,求m的值.
如图所示,若∠AOC=α,过点O点作射线OB,OE平分∠AOB,OF平分∠COB,若∠AOC=(5m+20)°,∠EOF=(m+40)°,求m的值.