题目内容
19. 如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为2m,梯子的顶端B到地面的距离为7m,现将梯子的底端A向外移动到A′,使梯子底端A′到墙根O的距离等于3m,同时梯子的顶端B下降到B′,那么BB′=7-2$\sqrt{11}$m.
如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为2m,梯子的顶端B到地面的距离为7m,现将梯子的底端A向外移动到A′,使梯子底端A′到墙根O的距离等于3m,同时梯子的顶端B下降到B′,那么BB′=7-2$\sqrt{11}$m.
分析 由题意可知OA=2,OB=7,先利用勾股定理求出AB,梯子移动过程中长短不变,所以AB=A′B′,又由题意可知OA′=3,利用勾股定理分别求OB′长,把其相减得解.
解答 解:在直角三角形AOB中,因为OA=2m,OB=7m,
由勾股定理得:AB=$\sqrt{{2}^{2}+{7}^{2}}$=$\sqrt{53}$m,
由题意可知AB=A′B′=$\sqrt{53}$m,
又∵OA′=3m,
根据勾股定理得:OB′=$\sqrt{53-{3}^{2}}$=$\sqrt{44}$=2$\sqrt{11}$m,
∴BB′=7-2$\sqrt{11}$(m).
故答案为:7-2$\sqrt{11}$.
点评 本题考查了勾股定理的应用,解答本题的关键是掌握勾股定理的表达式.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
7.已知a2-a=7,则代数式$\frac{a-1}{a+2}$•$\frac{{a}^{2}-4}{{a}^{2}-2a+1}$÷$\frac{1}{{a}^{2}-1}$的值是( )
| A. | 3 | B. | $\frac{7}{2}$ | C. | 4 | D. | 5 |
 已知数a,b,c在数轴上的位置如图所示,试化简|a-b|+|a+b+c|-|c-b|.
已知数a,b,c在数轴上的位置如图所示,试化简|a-b|+|a+b+c|-|c-b|.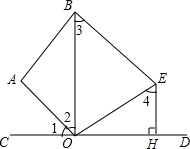 如图,已知∠1=∠2,OE⊥OA于点O,EH⊥CD于点H,∠3=∠4.求证:BE∥AO.
如图,已知∠1=∠2,OE⊥OA于点O,EH⊥CD于点H,∠3=∠4.求证:BE∥AO. 如图所示,CP是△ACB的角平分线,O是CP上任意一点,⊙O与AC相切于点E.求证:BC是⊙O的切线.
如图所示,CP是△ACB的角平分线,O是CP上任意一点,⊙O与AC相切于点E.求证:BC是⊙O的切线.