题目内容
4.A、B两家公司都准备向社会招聘人才,两家公司招聘条件基本相同,只有工资待遇有如下差异,A公司年薪50000元,从第二年起每年加工龄工资1000元,B公司半年年薪25000元,每半年加工龄工资500元.(1)求第2年A、B两家公司给应聘者的年薪;
(2)求第n年,A、B两家公司给应聘者的年薪;
(3)从经济收入角度考虑的话,选择哪家公司?
分析 (1)根据两家公司的工资待遇分别列出代数式求解即可.
(2)结合(1)中规律列出表示A,B两家公司招聘的工作人员第n年的工资收入的代数式即可.
(3)比较(2)中两代数式的大小即可得哪家公司有利
解答 解:(1)A公司第二年的年薪为50000+1000=51000元,
B公司第二年的年薪为25000×2+500×3=51500元,
(2)A公司第n年的年薪是50000+1000(n-1)=49000+1000n;
B公司第n年的年薪是25000×2+500(2n-1)=49500+1000n.
(3)由(2)知,A公司第n年的年薪是49000+1000n,B公司第n年的年薪是49500+1000n.
∴A、B公司第n年的年薪差为(49500+1000n)-(49000+1000n)=500元.
所以选择B公司有利.
点评 本题考查了列代数式及比较代数式的大小,解题的关键是根据题中的等量关系列出代数式.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
12.在物理并联电路里,支路电阻R1、R2与总电阻R之间的关系式为$\frac{1}{R}$=$\frac{1}{{R}_{1}}$+$\frac{1}{{R}_{2}}$,若R≠R1,用R、R1表示R2正确的是( )
| A. | R2=$\frac{R{R}_{1}}{R-{R}_{1}}$ | B. | R2=$\frac{R{R}_{1}}{{R}_{1}-R}$ | C. | R2=$\frac{{R}_{1}-R}{R{R}_{1}}$ | D. | R2=$\frac{R-{R}_{1}}{R{R}_{1}}$ |
19.在如图所示的3×3方阵图中,处于同一横行、同一竖列、同一斜对角线上的3个数之和都相等.现在方阵图
中已填写了一些数和代数式(其中每个代数式都表示一个数),则x的值为-1,空白处应填写的3个数的和为-4.
中已填写了一些数和代数式(其中每个代数式都表示一个数),则x的值为-1,空白处应填写的3个数的和为-4.
| -2 | -4 | 3x+6 |
| 4 | x | |
| -x-6 |
9.代数式ax2+bx+c(a≠0,a,b,c是常数)中,x与ax2+bx+c的对应值如下表:
请判断一元二次方程ax2+bx+c=0(a≠0,a,b,c是常数)的两个根x1,x2的取值范围是下列选项中的( )
| x | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 |
| ax2+bx+c | -2 | -$\frac{1}{4}$ | 1 | $\frac{7}{4}$ | 2 | $\frac{7}{4}$ | 1 | -$\frac{1}{4}$ | -2 |
| A. | -$\frac{1}{2}$<x1<0,$\frac{3}{2}$<x2<2 | B. | -1<x1<-$\frac{1}{2}$,2<x2<$\frac{5}{2}$ | ||
| C. | -$\frac{1}{2}$<x1<0,2<x2<$\frac{5}{2}$ | D. | -1<x1<-$\frac{1}{2}$,$\frac{3}{2}$<x2<2 |
13.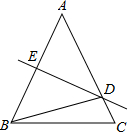 在△ABC中,AB=AC,∠A=50°,AB的垂直平分线DE交AC于D,垂足为E,则∠DBC的度数是( )
在△ABC中,AB=AC,∠A=50°,AB的垂直平分线DE交AC于D,垂足为E,则∠DBC的度数是( )
 在△ABC中,AB=AC,∠A=50°,AB的垂直平分线DE交AC于D,垂足为E,则∠DBC的度数是( )
在△ABC中,AB=AC,∠A=50°,AB的垂直平分线DE交AC于D,垂足为E,则∠DBC的度数是( )| A. | 50° | B. | 40° | C. | 65° | D. | 15° |
14.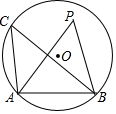 如图,AB是⊙O的弦,点C在⊙O上,∠ACB=40°,点P在⊙O的内部,且点C、点P在AB同侧,则∠APB的角度是( )
如图,AB是⊙O的弦,点C在⊙O上,∠ACB=40°,点P在⊙O的内部,且点C、点P在AB同侧,则∠APB的角度是( )
 如图,AB是⊙O的弦,点C在⊙O上,∠ACB=40°,点P在⊙O的内部,且点C、点P在AB同侧,则∠APB的角度是( )
如图,AB是⊙O的弦,点C在⊙O上,∠ACB=40°,点P在⊙O的内部,且点C、点P在AB同侧,则∠APB的角度是( )| A. | 大于40° | B. | 等于40° | C. | 小于40° | D. | 无法确定 |
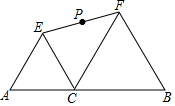 如图,线段AB=2,C是AB上一动点,以AC、BC为边在AB同侧作正△ACE、正△BCF,连EF,点P为EF的中点.当点C从A运动到B时,P点运动路径长为1.
如图,线段AB=2,C是AB上一动点,以AC、BC为边在AB同侧作正△ACE、正△BCF,连EF,点P为EF的中点.当点C从A运动到B时,P点运动路径长为1.