题目内容
9.代数式ax2+bx+c(a≠0,a,b,c是常数)中,x与ax2+bx+c的对应值如下表:| x | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 |
| ax2+bx+c | -2 | -$\frac{1}{4}$ | 1 | $\frac{7}{4}$ | 2 | $\frac{7}{4}$ | 1 | -$\frac{1}{4}$ | -2 |
| A. | -$\frac{1}{2}$<x1<0,$\frac{3}{2}$<x2<2 | B. | -1<x1<-$\frac{1}{2}$,2<x2<$\frac{5}{2}$ | ||
| C. | -$\frac{1}{2}$<x1<0,2<x2<$\frac{5}{2}$ | D. | -1<x1<-$\frac{1}{2}$,$\frac{3}{2}$<x2<2 |
分析 观察表格可知,在x<1时,随x值的增大,代数式ax2+bx+c的值逐渐增大,x的值在-$\frac{1}{2}$~0之间,代数式ax2+bx+c的值由负到正,故可判断ax2+bx+c=0时,对应的x的值在-$\frac{1}{2}$~0之间,在x>1时,随x的值增大,代数式ax2+bx+c逐渐减小,x的值在2~$\frac{5}{2}$之间,代数式ax2+bx+c的值由正到负,故可判断ax2+bx+c=0时,对应的x的值在2~$\frac{5}{2}$之间,
解答 解:根据表格可知,代数式ax2+bx+c=0时,对应的x的值在-$\frac{1}{2}$~0和2~$\frac{5}{2}$之间,
即:一元二次方程ax2+bx+c=0(a≠0,a,b,c是常数)的两个根x1,x2的取值范围是-$\frac{1}{2}$<x1<0,2<x2<$\frac{5}{2}$
故选C.
点评 本题考查了一元二次方程的解,关键是观察表格,确定代数式值由负到正时,对应的x的取值范围.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.1+22+33+…+20172017的末位数字是( )
| A. | 1 | B. | 3 | C. | 5 | D. | 6 |
17.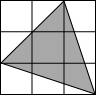 如图,阴影部分面积占整个大正方形面积的( )
如图,阴影部分面积占整个大正方形面积的( )
 如图,阴影部分面积占整个大正方形面积的( )
如图,阴影部分面积占整个大正方形面积的( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{9}$ | D. | $\frac{4}{9}$ |
 如图所示,小华从点A出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地点A时,走的路程一共是150米.
如图所示,小华从点A出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地点A时,走的路程一共是150米.