题目内容
14.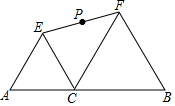 如图,线段AB=2,C是AB上一动点,以AC、BC为边在AB同侧作正△ACE、正△BCF,连EF,点P为EF的中点.当点C从A运动到B时,P点运动路径长为1.
如图,线段AB=2,C是AB上一动点,以AC、BC为边在AB同侧作正△ACE、正△BCF,连EF,点P为EF的中点.当点C从A运动到B时,P点运动路径长为1.
分析 分别延长AE、BF交于点H,得出P为CH中点,则P的运行轨迹为三角形HAB的中位线MN.运用中位线的性质求出MN的长度即可.
解答 解:如图,分别延长AE、BF交于点H.
∵∠A=∠FCB=60°,
∴AH∥CF,
∵∠B=∠ECA=60°,
∴CE∥BH,
∴四边形ECFH为平行四边形,
∴EF与HC互相平分.
∵P为CH的中点,
∴P正好为EF中点,即在P的运动过程中,P始终为CH的中点,所以P的运行轨迹为三角形HAB的中位线MN.
∵AB=2,
∴MN=1,即P的移动路径长为1,
故答案为:1
点评 本题考查了轨迹问题,关键是根据等边三角形及中位线的性质,以及动点问题解答.

练习册系列答案
相关题目
2.$\sqrt{36}$等于( )
| A. | ±6 | B. | 6 | C. | ±$\sqrt{6}$ | D. | $\sqrt{6}$ |
9.已知实数x,y满足|x-4|+$\sqrt{y-8}$=0,则以x,y的值为两边长的等腰三角形的周长为( )
| A. | 20或16 | B. | 20 | C. | 16 | D. | 以上答案均不对 |
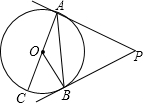 如图,PA、PB是⊙O的两条切线,A、B是切点,AC是⊙O的直径,∠BAC=35°,求∠P的度数.
如图,PA、PB是⊙O的两条切线,A、B是切点,AC是⊙O的直径,∠BAC=35°,求∠P的度数. 如图所示,小华从点A出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地点A时,走的路程一共是150米.
如图所示,小华从点A出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地点A时,走的路程一共是150米.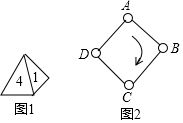 如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4,如图2,正方形ABCD顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.
如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4,如图2,正方形ABCD顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.