题目内容
17.如图,线段AB绕点O顺时针旋转一定的角度得到线段A1B1.(1)请用直尺和圆规作出旋转中心O(不写作法,保留作图痕迹);
(2)连接OA、OA1、OB、OB1,如果∠AO A1=∠BOB1=α;OA=OA1=a;OB=OB1=b.则线段AB扫过的面积是$\frac{α•π•({b}^{2}-{a}^{2})}{360}$.
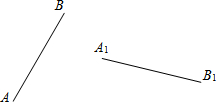
分析 (1)先连结AA1和BB1,然后分别作它们的垂直平分线,则两垂直平分线的交点即为点O;
(2)根据扇形面积公式,利用线段AB扫过的面积=S扇形BOB1-S扇形AOA1进行计算即可.
解答 解:(1)如图,点O为所作;
(2)线段AB扫过的面积=S扇形BOB1-S扇形AOA1=$\frac{α•π•{b}^{2}}{360}$-$\frac{α•π•{a}^{2}}{360}$=$\frac{α•π•({b}^{2}-{a}^{2})}{360}$.
故答案为$\frac{α•π•({b}^{2}-{a}^{2})}{360}$.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了扇形面积公式.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
12. 如图,在△ABC中,BC=6,∠A=90°,∠B=70°.把△ABC沿BC方向平移到△DEF的位置,若CF=2,则下列结论中错误的是( )
如图,在△ABC中,BC=6,∠A=90°,∠B=70°.把△ABC沿BC方向平移到△DEF的位置,若CF=2,则下列结论中错误的是( )
 如图,在△ABC中,BC=6,∠A=90°,∠B=70°.把△ABC沿BC方向平移到△DEF的位置,若CF=2,则下列结论中错误的是( )
如图,在△ABC中,BC=6,∠A=90°,∠B=70°.把△ABC沿BC方向平移到△DEF的位置,若CF=2,则下列结论中错误的是( )| A. | BE=2 | B. | ∠F=20° | C. | AB∥DE | D. | DF=6 |
2.满足下列条件的三角形中,不是直角三角形的是( )
| A. | 三内角之比为1:2:3 | B. | 三边长的平方之比为1:2:3 | ||
| C. | 三边长之比为3:4:5 | D. | 三内角之比为3:4:5 |
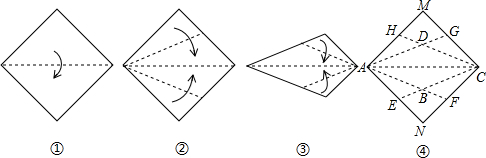 在折纸这种传统手工艺术中,蕴含许多数学思想,我们可以通过折纸得到一些特殊图形,把一张正方形纸片按照图①~④的过程折叠后展开.
在折纸这种传统手工艺术中,蕴含许多数学思想,我们可以通过折纸得到一些特殊图形,把一张正方形纸片按照图①~④的过程折叠后展开. 如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N,若∠BAD=∠BCD=120°,AM=AN=$\sqrt{3}$,
如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N,若∠BAD=∠BCD=120°,AM=AN=$\sqrt{3}$, 如图,直线AB,CD相交于点O,EO⊥AB,垂足为点O,若∠AOD=132°,则∠EOC=42°.
如图,直线AB,CD相交于点O,EO⊥AB,垂足为点O,若∠AOD=132°,则∠EOC=42°.