题目内容
7.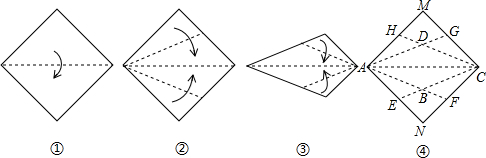 在折纸这种传统手工艺术中,蕴含许多数学思想,我们可以通过折纸得到一些特殊图形,把一张正方形纸片按照图①~④的过程折叠后展开.
在折纸这种传统手工艺术中,蕴含许多数学思想,我们可以通过折纸得到一些特殊图形,把一张正方形纸片按照图①~④的过程折叠后展开.求证:四边形ABCD是菱形.
分析 根据折叠的性质得到∠MAD=∠DAC=$\frac{1}{2}$∠MAC,∠CAB=∠NAB=$\frac{1}{2}$∠CAN,∠DCA=∠MCD=$\frac{1}{2}$∠ACM,∠ACB=∠NCB=$\frac{1}{2}$∠ACN,再根据正方形的性质得∠MAC=∠∠MCA=∠NAC=∠NCA,所以∠DAC=∠BAC=∠BCA=∠DCA,于是可判断四边形ABCD为平行四边形,且DA=DC,然后根据菱形的判定方法得到四边形ABCD为菱形.
解答 解:∵△AMG沿AG折叠,使AM落在AC上,
∴∠MAD=∠DAC=$\frac{1}{2}$∠MAC,
同理可得∠CAB=∠NAB=$\frac{1}{2}$∠CAN,∠DCA=∠MCD=$\frac{1}{2}$∠ACM,∠ACB=∠NCB=$\frac{1}{2}$∠ACN,
∵四边形AMCN是正方形,
∴∠MAC=∠MCA=∠NAC=∠NCA,
∴∠DAC=∠BAC=∠BCA=∠DCA
∴AD∥BC,AB∥DC,
∴四边形ABCD为平行四边形,
∵∠DAC=∠DCA,
∴AD=CD,
∴四边形ABCD为菱形.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了菱形的判定方法以及正方形的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.∠α的余角为65°,则∠α的度数为( )
| A. | 35° | B. | 25° | C. | 45° | D. | 65° |
15.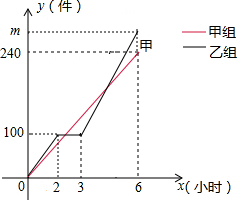 甲、乙两组工人同时加工某种零件,乙组在工作中有一次停产更换设备,之后乙组的工作效率是原来的1.2倍,甲、乙两组加工出的零件合在一起装箱,每200件装一箱,零件装箱的时间忽略不计,两组各自加工零件的数量y(件)与时间x(时)的函数图象如图,以下说法错误的是( )
甲、乙两组工人同时加工某种零件,乙组在工作中有一次停产更换设备,之后乙组的工作效率是原来的1.2倍,甲、乙两组加工出的零件合在一起装箱,每200件装一箱,零件装箱的时间忽略不计,两组各自加工零件的数量y(件)与时间x(时)的函数图象如图,以下说法错误的是( )
 甲、乙两组工人同时加工某种零件,乙组在工作中有一次停产更换设备,之后乙组的工作效率是原来的1.2倍,甲、乙两组加工出的零件合在一起装箱,每200件装一箱,零件装箱的时间忽略不计,两组各自加工零件的数量y(件)与时间x(时)的函数图象如图,以下说法错误的是( )
甲、乙两组工人同时加工某种零件,乙组在工作中有一次停产更换设备,之后乙组的工作效率是原来的1.2倍,甲、乙两组加工出的零件合在一起装箱,每200件装一箱,零件装箱的时间忽略不计,两组各自加工零件的数量y(件)与时间x(时)的函数图象如图,以下说法错误的是( )| A. | 甲组加工零件数量y与时间x的关系式为y甲=40x | |
| B. | 乙组加工零件总量m=280 | |
| C. | 经过2$\frac{1}{2}$小时恰好装满第1箱 | |
| D. | 经过4$\frac{3}{4}$小时恰好装满第2箱 |
2.当a=-1时,分式$\frac{{{a^2}+a}}{{{a^2}-a}}$( )
| A. | 等于零 | B. | 等于1 | C. | 等于-1 | D. | 没有意义 |
19.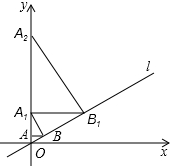 如图,直线l为正比例函数y=$\frac{\sqrt{3}}{3}$x的图象,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点Bn的坐标是( )
如图,直线l为正比例函数y=$\frac{\sqrt{3}}{3}$x的图象,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点Bn的坐标是( )
 如图,直线l为正比例函数y=$\frac{\sqrt{3}}{3}$x的图象,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点Bn的坐标是( )
如图,直线l为正比例函数y=$\frac{\sqrt{3}}{3}$x的图象,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点Bn的坐标是( )| A. | ($\sqrt{3}$×4n,4n) | B. | ($\sqrt{3}$×4n-1,4n-1) | C. | ($\sqrt{3}$×4n-1,4n) | D. | ($\sqrt{3}$×4n,4n-1) |
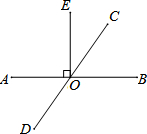 如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC:∠AOD=7:11,求∠DOE的度数.
如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC:∠AOD=7:11,求∠DOE的度数.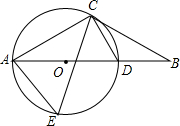 如图,在△ABC中,AC=BC,∠CAB=30°,过点C作CD⊥AC交AB于点D,⊙O是△ACD的外接圆.
如图,在△ABC中,AC=BC,∠CAB=30°,过点C作CD⊥AC交AB于点D,⊙O是△ACD的外接圆. 如图是边长为2的正方形ABCD,对角线为AC,△ABC以点A为中心,顺时针旋转45°得△AB′C′,则图中阴影部分的面积为4$\sqrt{2}$-4.
如图是边长为2的正方形ABCD,对角线为AC,△ABC以点A为中心,顺时针旋转45°得△AB′C′,则图中阴影部分的面积为4$\sqrt{2}$-4.