题目内容
5. 如图,△ABC中,∠CAB=90°,AC=AB,AO是高,CE平分∠ACO交AO于E,把△CAE沿CA折叠得△CAD,F是CE的中点,连接FD、FB.若AE=2,则S四边形FDAB=6+3$\sqrt{2}$.
如图,△ABC中,∠CAB=90°,AC=AB,AO是高,CE平分∠ACO交AO于E,把△CAE沿CA折叠得△CAD,F是CE的中点,连接FD、FB.若AE=2,则S四边形FDAB=6+3$\sqrt{2}$.
分析 连接DE、BE,根据折叠的性质得:AC是DE的垂直平分线,∠DAC=∠CAO,AD=AE=2,得△ADE是等腰直角三角形,利用勾股定理计算DE=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,则DG=EG=$\sqrt{2}$,易证△GCE≌△OCE,所以CG=CO,CG=AO=2+$\sqrt{2}$,根据三角形的中线将三角形分成面积相等的两部分可知:S△EFB=S△EOB,S△EFD=S△EGC,将所求四边形面积分成四个三角形面积的和进行计算即可.
解答 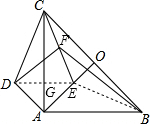 解:连接DE、BE,
解:连接DE、BE,
由折叠得:AC是DE的垂直平分线,∠DAC=∠CAO,AD=AE=2,
∵△ACB是等腰直角三角形,AO是高,
∴CO=BO,∠CAO=45°,
∴∠DAC=45°,
∴∠DAE=90°,
由勾股定理得:DE=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∴DG=EG=$\sqrt{2}$,
∵△AGE是等腰直角三角形,
∴AG=$\sqrt{2}$,
∵CE平分∠ACB,EG⊥AC,EO⊥BC,
∴OE=EG=$\sqrt{2}$,
易证△GCE≌△OCE,
∴CG=CO,
设CG=x,则CO=x,
∵△ACO是等腰直角三角形,
∴CO=AO=AE+EO,
即x=2+$\sqrt{2}$,
∴CG=2+$\sqrt{2}$,
∵F是CE的中点,O是BC的中点,
∴S△EFB=$\frac{1}{2}$S△BEC,S△EOB=$\frac{1}{2}$S△BEC,
∴S△EFB=S△EOB,
同理可得:S△EFD=S△EGC,
∴S四边形FDAB=S△ADE+S△EFD+S△ABE+S△BEF,
=$\frac{1}{2}$AE•AD+S△EGC+S△ABE+S△EOB,
=$\frac{1}{2}$×2×2+$\frac{1}{2}$EG•CG+S△AOB,
=2+$\frac{1}{2}$×$\sqrt{2}×(2+\sqrt{2})$+$\frac{1}{2}$(2+$\sqrt{2}$)2,
=2+$\sqrt{2}$+1+3+2$\sqrt{2}$,
=6+3$\sqrt{2}$,
故答案为:6+3$\sqrt{2}$.
点评 本题考查了三角形全等的性质和判定、等腰直角三角形的性质和判定、三角形中线及等腰三角形的三线合一的性质,熟练掌握三角形的中线将三角形面积平分这一性质是本题的关键,最后利用了求和法求不规则四边形的面积.

 在下列有理数运算中,不能借助下面数轴解释的是( )
在下列有理数运算中,不能借助下面数轴解释的是( )| A. | (-3)+(-3)=-6 | B. | (-3)×2=-6 | C. | 2×(-3)=-6 | D. | 3×(-2)=-6 |
| A. | 0是单项式 | B. | 单项式x2y的次数是2 | ||
| C. | 多项式ab+3是一次二项式 | D. | 单项式-$\frac{1}{3}$πx2y的系数是-$\frac{1}{3}$ |
 如图,在△ABC中,中线BE,CD相交于点O,连接DE,则下列判断错误的是( )
如图,在△ABC中,中线BE,CD相交于点O,连接DE,则下列判断错误的是( )| A. | DE是△ABC的中位线 | B. | 点O是△ABC的重心 | ||
| C. | △DEO∽△CBO | D. | $\frac{{S}_{△DOE}}{{S}_{△ADE}}$=$\frac{1}{2}$ |
| 每天零花钱(元) | 0 | 5 | 10 | 15 | 20 |
| 人数 | 2 | 3 | 2 | 6 | 2 |
| A. | 众数是20元 | B. | 平均数是11元 | C. | 极差是15元 | D. | 中位数是10元 |