题目内容
15.已知实数在数轴上的位置如图所示,化筒:|a-b|-$\sqrt{{a}^{2}}$+($\sqrt{-b}$)2+2$\root{3}{{b}^{3}}$.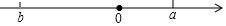
分析 根据数轴上点的位置判断出a-b,a,b的正负,原式利用平方根、立方根定义,以及绝对值的代数意义化简,即可得到结果.
解答 解:根据数轴上点的位置得:b<0<a,且|a|<|b|,
∴a-b>0,
则原式=a-b-a-b+2b=0.
点评 此题考查了实数的运算,以及实数与数轴,判断出各式的正负是解本题的关键.

练习册系列答案
相关题目
6.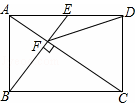 如图,点E是矩形ABCD的边AD的中点,且BE⊥AC于点F,则下列结论中错误的是( )
如图,点E是矩形ABCD的边AD的中点,且BE⊥AC于点F,则下列结论中错误的是( )
 如图,点E是矩形ABCD的边AD的中点,且BE⊥AC于点F,则下列结论中错误的是( )
如图,点E是矩形ABCD的边AD的中点,且BE⊥AC于点F,则下列结论中错误的是( )| A. | AF=$\frac{1}{2}$CF | B. | ∠DCF=∠DFC | ||
| C. | 图中与△AEF相似的三角形共有4个 | D. | tan∠CAD=$\frac{\sqrt{2}}{2}$ |
3. 如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD,若CD=AC,∠B=25°,则∠ACB的度数为( )
如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD,若CD=AC,∠B=25°,则∠ACB的度数为( )
 如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD,若CD=AC,∠B=25°,则∠ACB的度数为( )
如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD,若CD=AC,∠B=25°,则∠ACB的度数为( )| A. | 105° | B. | 100° | C. | 95° | D. | 90° |
10.在-1,0,1,2,3这五个数中任取两数m,n,则二次函数y=-(x+m)2-n的顶点在x轴上的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
4.已知圆锥的底面半径为4,母线长为12,则圆锥的侧面展开图的圆心角为( )
| A. | 60° | B. | 90° | C. | 120° | D. | 216° |
 如图,△ABC中,∠CAB=90°,AC=AB,AO是高,CE平分∠ACO交AO于E,把△CAE沿CA折叠得△CAD,F是CE的中点,连接FD、FB.若AE=2,则S四边形FDAB=6+3$\sqrt{2}$.
如图,△ABC中,∠CAB=90°,AC=AB,AO是高,CE平分∠ACO交AO于E,把△CAE沿CA折叠得△CAD,F是CE的中点,连接FD、FB.若AE=2,则S四边形FDAB=6+3$\sqrt{2}$.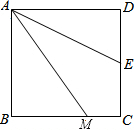 如图,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
如图,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM. 如图,以等腰三角形ABC的底边BC为直径的圆O分别交两腰于D、E,连结DE,求证:
如图,以等腰三角形ABC的底边BC为直径的圆O分别交两腰于D、E,连结DE,求证: