题目内容
14. 如图,在△AOB中,OA=OB,∠AOB=50°,将△AOB绕O点顺时针旋转30°,得到△COD,OC交AB于点F,CD分别交AB、OB于点E、H.求证:EF=EH.
如图,在△AOB中,OA=OB,∠AOB=50°,将△AOB绕O点顺时针旋转30°,得到△COD,OC交AB于点F,CD分别交AB、OB于点E、H.求证:EF=EH.
分析 根据等腰三角形的性质,可得∠A与∠B,根据旋转的性质,可得∠AOC=∠BOD=30°,OD=OB=OA,∠D=∠B,根据全等三角形的判定与性质,可得答案.
解答 证明:∵OA=OB,∠AOB=50°,
∴∠A=∠B.
∵将△AOB绕O点顺时针旋转30°,得到△COD,
∴∠AOC=∠BOD=30°,OD=OB=OA,∠D=∠B.
在△AOF和△DOH中,
$\left\{\begin{array}{l}{∠A=∠D}\\{AO=DO}\\{∠AOF=∠DOH}\end{array}\right.$,
∴△AOF≌△DOH(ASA),
∴OF=OH,
∵OC=OB,
∴FC=BH.
在△FCE和△HBE中,
$\left\{\begin{array}{l}{∠C=∠B}\\{∠CEF=∠BEH}\\{CF=BH}\end{array}\right.$,
∴△FCE≌△HBE(AAS),
∴EF=EH.
点评 本题考查了旋转的性质,利用旋转的性质得出∠AOC=∠BOD=30°,OD=OB=OA,∠D=∠B是解题关键,又利用了全等三角形的判定与性质.

练习册系列答案
相关题目
4.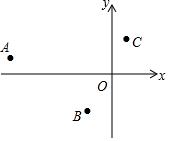 在平面直角坐标系xOy中,二次函数y=ax2+bx的图象经过点A,B,C,则对系数a和b判断正确的是( )
在平面直角坐标系xOy中,二次函数y=ax2+bx的图象经过点A,B,C,则对系数a和b判断正确的是( )
 在平面直角坐标系xOy中,二次函数y=ax2+bx的图象经过点A,B,C,则对系数a和b判断正确的是( )
在平面直角坐标系xOy中,二次函数y=ax2+bx的图象经过点A,B,C,则对系数a和b判断正确的是( )| A. | a>0,b>0 | B. | a<0,b<0 | C. | a>0,b<0 | D. | a<0,b>0 |
 已知△ABC分别以△ABC的AC,BC边为腰,A,B为直角顶点,作等腰Rt△ACE和等腰Rt△BCD,M为ED的中点,求证:AM⊥BM.
已知△ABC分别以△ABC的AC,BC边为腰,A,B为直角顶点,作等腰Rt△ACE和等腰Rt△BCD,M为ED的中点,求证:AM⊥BM.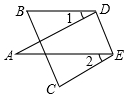 如图所示,将纸片△ABC沿着DE折叠压平,则∠A,∠1与∠2之间的数量关系是∠A=$\frac{1}{2}$(∠1+∠2).
如图所示,将纸片△ABC沿着DE折叠压平,则∠A,∠1与∠2之间的数量关系是∠A=$\frac{1}{2}$(∠1+∠2). 如图,已知线段AB、a、b,请用尺规按下列要求作图:
如图,已知线段AB、a、b,请用尺规按下列要求作图: 作图:已知∠AOB,试在∠AOB内确定一点P,使P到OA、OB的距离相等,并且到M、N两点的距离也相等.
作图:已知∠AOB,试在∠AOB内确定一点P,使P到OA、OB的距离相等,并且到M、N两点的距离也相等.