题目内容
15.若方程组$\left\{\begin{array}{l}{2{x}^{2}+m{y}^{{m}^{2}-2m-1}=2}\\{5{x}^{2}-3xy=4}\end{array}\right.$是二元二次方程组,求m的值.分析 根据二元二次方程组的概念可得m2-2m-1=0或m2-2m-1=1或m2-2m-1=2,分别解关于m的方程可得.
解答 解:根据题意,m2-2m-1=0或m2-2m-1=1或m2-2m-1=2,
解m2-2m-1=0,得:m=1$±\sqrt{2}$,
解m2-2m-1=1,得:m=1$±\sqrt{3}$,
解m2-2m-1=2,得:m=3或-1.
综上,m的值为1$±\sqrt{2}$,1$±\sqrt{3}$,3或-1.
点评 本题考查了高次方程组,根据方程组的定义把方程组转化成一元二次方程是解此题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
5. 如图所示,将纸片△ABC沿着DE折叠压平,则( )
如图所示,将纸片△ABC沿着DE折叠压平,则( )
 如图所示,将纸片△ABC沿着DE折叠压平,则( )
如图所示,将纸片△ABC沿着DE折叠压平,则( )| A. | ∠A=∠1+∠2 | B. | ∠A=$\frac{1}{2}$(∠1+∠2) | C. | ∠A=$\frac{1}{3}$(∠1+∠2) | D. | ∠A=$\frac{1}{4}$(∠1+∠2) |
20.若菱形的周长为8,高为$\sqrt{2}$,则菱形两邻角的度数比为( )
| A. | 2:1 | B. | 3:1 | C. | 4:1 | D. | 5:1 |
4.实数-5,0,$-\sqrt{3}$,3中最大的数是( )
| A. | 3 | B. | 0 | C. | $-\sqrt{3}$ | D. | -5 |
 如图,在?ABCD中,E是AD上的一点,已知AE:ED=2:1,AO=4,求OC的长.
如图,在?ABCD中,E是AD上的一点,已知AE:ED=2:1,AO=4,求OC的长. 如图,已知直线AB∥DE.
如图,已知直线AB∥DE.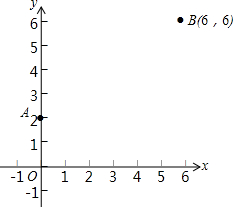 如图,已知A(0,2),B(6,6),x轴上一点C到A,B的距离之和为最小,求C点的坐标.
如图,已知A(0,2),B(6,6),x轴上一点C到A,B的距离之和为最小,求C点的坐标.