题目内容
7.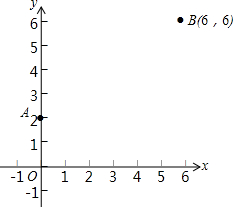 如图,已知A(0,2),B(6,6),x轴上一点C到A,B的距离之和为最小,求C点的坐标.
如图,已知A(0,2),B(6,6),x轴上一点C到A,B的距离之和为最小,求C点的坐标.
分析 如图作点A关于x轴的对称点F(0,-2),求出直线BF与x轴的交点即可.
解答 解: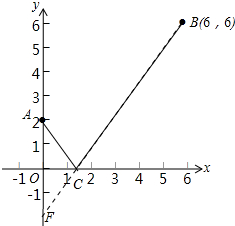 如图作点A关于x轴的对称点F(0,-2),
如图作点A关于x轴的对称点F(0,-2),
连接BF与x轴的交点为C,此时AC+BC最短.
设直线BF为y=kx+b,把B、F两点坐标代入得$\left\{\begin{array}{l}{6k+b=6}\\{b=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=-2}\end{array}\right.$,
∴直线BF为y=$\frac{4}{3}$x-2,令y=0,x=$\frac{3}{2}$,
∴点C坐标($\frac{3}{2}$,0).
点评 本题考查坐标与图形、轴对称-最小值问题等知识,解题的关键是利用一次函数的性质解决问题,学会转化的思想,把问题转化为求函数与x轴的交点问题,属于中考常考题型.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
19. 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,AD=6,AB=8,则$\frac{AF}{FC}$=( )
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,AD=6,AB=8,则$\frac{AF}{FC}$=( )
 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,AD=6,AB=8,则$\frac{AF}{FC}$=( )
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,AD=6,AB=8,则$\frac{AF}{FC}$=( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
16.若点A(x1,y1),B(x2,y2),和C(x3,y3),分别在反比例函数$y=\frac{6}{x}$的图象上,且x1<x2<0<x3,则下列判断中正确的是( )
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y2<y1 | D. | y2<y3<y1 |
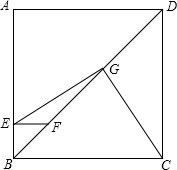 已知正方形ABCD,点F为射线DB上一点,过点F作FE∥AD,FE交射线AB于E,G为FD的中点,连接CG,求证:∠CGE=90°.
已知正方形ABCD,点F为射线DB上一点,过点F作FE∥AD,FE交射线AB于E,G为FD的中点,连接CG,求证:∠CGE=90°.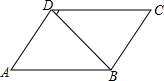 已知:平行四边形ABCD,BD为对角线(如图)∠A=70°,∠BDC=30°,AD=15.求:∠C,∠ADB的度数,并求BC边的长.
已知:平行四边形ABCD,BD为对角线(如图)∠A=70°,∠BDC=30°,AD=15.求:∠C,∠ADB的度数,并求BC边的长.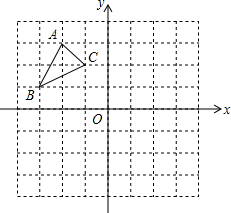 如图,△ABC中A(-2,3),B(-3,1),C(-1,2)
如图,△ABC中A(-2,3),B(-3,1),C(-1,2)