题目内容
16．
如图，已知扇形AOB的半径为10公分，圆心角为54°，则此扇形面积为多少平方公分？（ ）| A． | 100π | B． | 20π | C． | 15π | D． | 5π |
分析 利用扇形面积公式计算即可得到结果．
解答 解：∵扇形AOB的半径为10公分，圆心角为54°，
∴S扇形AOB=$\frac{54π×1{0}^{2}}{360}$=15π（平方公分），
故选C．
点评 此题考查了扇形面积的计算，熟练掌握扇形面积公式是解本题的关键．
练习册系列答案
相关题目
6．一个不透明布袋里装有1个白球、2个黑球、3个红球，它们除颜色外均相同．从中任意摸出一个球，则是红球的概率为（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
7．2016年第一季度，我市“蓝天白云、繁星闪烁”天数持续增加，获得山东省环境空气质量生态补偿资金408万元，408万用科学记数法表示正确的是（ ）
| A． | 408×104 | B． | 4.08×104 | C． | 4.08×105 | D． | 4.08×106 |
4．若满足不等式20＜5-2（2+2x）＜50的最大整数解为a，最小整数解为b，则a+b之值为何？（ ）
| A． | -15 | B． | -16 | C． | -17 | D． | -18 |
11．
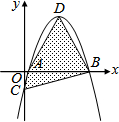如图，坐标平面上，二次函数y=-x2+4x-k的图形与x轴交于A、B两点，与y轴交于C点，其顶点为D，且k＞0．若△ABC与△ABD的面积比为1：4，则k值为何？（ ）
如图，坐标平面上，二次函数y=-x2+4x-k的图形与x轴交于A、B两点，与y轴交于C点，其顶点为D，且k＞0．若△ABC与△ABD的面积比为1：4，则k值为何？（ ）| A． | 1 | B． | $\frac{1}{2}$ | C． | $\frac{4}{3}$ | D． | $\frac{4}{5}$ |
1．小昱和阿帆均从同一本书的第1页开始，逐页依顺序在每一页上写一个数．小昱在第1页写1，且之后每一页写的数均为他在前一页写的数加2；阿帆在第1页写1，且之后每一页写的数均为他在前一页写的数加7．若小昱在某页写的数为101，则阿帆在该页写的数为何？（ ）
| A． | 350 | B． | 351 | C． | 356 | D． | 358 |
8．
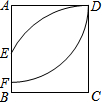如图，以矩形ABCD的A为圆心，AD长为半径画弧，交AB于F点；再以C为圆心，CD长为半径画弧，交AB于E点．若AD=5，CD=$\frac{17}{3}$，则EF的长度为何？（ ）
如图，以矩形ABCD的A为圆心，AD长为半径画弧，交AB于F点；再以C为圆心，CD长为半径画弧，交AB于E点．若AD=5，CD=$\frac{17}{3}$，则EF的长度为何？（ ）| A． | 2 | B． | 3 | C． | $\frac{2}{3}$ | D． | $\frac{7}{3}$ |
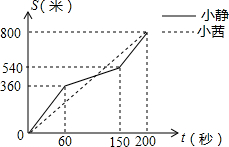为增强学生体质，某中学在体育课中加强了学生的长跑训练．在一次女子800米耐力测试中，小静和小茜在校园内200米的环形跑道上同时起跑，同时到达终点；所跑的路程S（米）与所用的时间t（秒）之间的函数图象如图所示，则她们第一次相遇的时间是起跑后的第120秒．
在平面直角坐标系中，一次函数y=ax+b（a≠0）的图形与反比例函数y=$\frac{k}{x}$（k≠0）的图象交于第二、四象限内的A、B两点，与y轴交于C点，过点A作AH⊥y轴，垂足为H，OH=3，tan∠AOH=$\frac{4}{3}$，点B的坐标为（m，-2）．