题目内容
4.若满足不等式20<5-2(2+2x)<50的最大整数解为a,最小整数解为b,则a+b之值为何?( )| A. | -15 | B. | -16 | C. | -17 | D. | -18 |
分析 根据不等式20<5-2(2+2x)<50可以求得x的取值范围,从而可以得到a、b的值,进而求得a+b的值.
解答 解:∵20<5-2(2+2x)<50,
解得,$-\frac{49}{4}<x<-\frac{19}{4}$,
∵不等式20<5-2(2+2x)<50的最大整数解为a,最小整数解为b,
∴a=-5,b=-12,
∴a+b=(-5)+(-12)=-17,
故选C.
点评 本题考查一元一次不等式组的整数解,解题的关键是明确解一元一次不等式组的方法.

练习册系列答案
相关题目
12.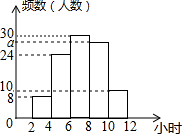 某校为了解全校同学五一假期参加社团活动的情况,抽查了100名同学,统计它们假期参加社团活动的时间,绘成频数分布直方图(如图),则参加社团活动时间的中位数所在的范围是( )
某校为了解全校同学五一假期参加社团活动的情况,抽查了100名同学,统计它们假期参加社团活动的时间,绘成频数分布直方图(如图),则参加社团活动时间的中位数所在的范围是( )
 某校为了解全校同学五一假期参加社团活动的情况,抽查了100名同学,统计它们假期参加社团活动的时间,绘成频数分布直方图(如图),则参加社团活动时间的中位数所在的范围是( )
某校为了解全校同学五一假期参加社团活动的情况,抽查了100名同学,统计它们假期参加社团活动的时间,绘成频数分布直方图(如图),则参加社团活动时间的中位数所在的范围是( )| A. | 4-6小时 | B. | 6-8小时 | C. | 8-10小时 | D. | 不能确定 |
16. 如图,已知扇形AOB的半径为10公分,圆心角为54°,则此扇形面积为多少平方公分?( )
如图,已知扇形AOB的半径为10公分,圆心角为54°,则此扇形面积为多少平方公分?( )
 如图,已知扇形AOB的半径为10公分,圆心角为54°,则此扇形面积为多少平方公分?( )
如图,已知扇形AOB的半径为10公分,圆心角为54°,则此扇形面积为多少平方公分?( )| A. | 100π | B. | 20π | C. | 15π | D. | 5π |
13. 如图,直线a,b被直线c所截,且a∥b,若∠1=55°,则∠2等于( )
如图,直线a,b被直线c所截,且a∥b,若∠1=55°,则∠2等于( )
 如图,直线a,b被直线c所截,且a∥b,若∠1=55°,则∠2等于( )
如图,直线a,b被直线c所截,且a∥b,若∠1=55°,则∠2等于( )| A. | 35° | B. | 45° | C. | 55° | D. | 125° |
14. 如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=80°,则∠1等于( )
如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=80°,则∠1等于( )
 如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=80°,则∠1等于( )
如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=80°,则∠1等于( )| A. | 120° | B. | 110° | C. | 100° | D. | 80° |
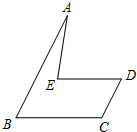 如图,已知AB∥CD,BC∥DE.若∠A=20°,∠C=120°,则∠AED的度数是80°.
如图,已知AB∥CD,BC∥DE.若∠A=20°,∠C=120°,则∠AED的度数是80°.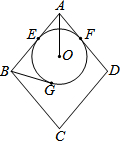 如图,菱形ABCD的边长为10,圆O分别与AB、AD相切于E、F两点,且与BG相切于G点.若AO=5,且圆O的半径为3,则BG的长度为何?( )
如图,菱形ABCD的边长为10,圆O分别与AB、AD相切于E、F两点,且与BG相切于G点.若AO=5,且圆O的半径为3,则BG的长度为何?( )