题目内容
5.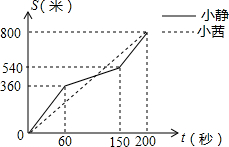 为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次女子800米耐力测试中,小静和小茜在校园内200米的环形跑道上同时起跑,同时到达终点;所跑的路程S(米)与所用的时间t(秒)之间的函数图象如图所示,则她们第一次相遇的时间是起跑后的第120秒.
为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次女子800米耐力测试中,小静和小茜在校园内200米的环形跑道上同时起跑,同时到达终点;所跑的路程S(米)与所用的时间t(秒)之间的函数图象如图所示,则她们第一次相遇的时间是起跑后的第120秒.
分析 分别求出OA、BC的解析式,然后联立方程,解方程就可以求出第一次相遇时间.
解答 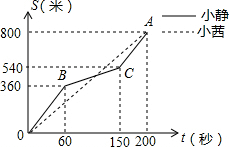 解:设直线OA的解析式为y=kx,
解:设直线OA的解析式为y=kx,
代入A(200,800)得800=200k,
解得k=4,
故直线OA的解析式为y=4x,
设BC的解析式为y1=k1x+b,由题意,得$\left\{\begin{array}{l}{360=60{k}_{1}+b}\\{540=150{k}_{1}+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=2}\\{b=240}\end{array}\right.$,
∴BC的解析式为y1=2x+240,
当y=y1时,4x=2x+240,
解得:x=120.
则她们第一次相遇的时间是起跑后的第120秒.
故答案为120.
点评 本题考查了一次函数的运用,一次函数的图象的意义的运用,待定系数法求一次函数的解析式的运用,解答时认真分析求出一次函数图象的数据意义是关键.

练习册系列答案
相关题目
16. 如图,已知扇形AOB的半径为10公分,圆心角为54°,则此扇形面积为多少平方公分?( )
如图,已知扇形AOB的半径为10公分,圆心角为54°,则此扇形面积为多少平方公分?( )
 如图,已知扇形AOB的半径为10公分,圆心角为54°,则此扇形面积为多少平方公分?( )
如图,已知扇形AOB的半径为10公分,圆心角为54°,则此扇形面积为多少平方公分?( )| A. | 100π | B. | 20π | C. | 15π | D. | 5π |
13. 如图,直线a,b被直线c所截,且a∥b,若∠1=55°,则∠2等于( )
如图,直线a,b被直线c所截,且a∥b,若∠1=55°,则∠2等于( )
 如图,直线a,b被直线c所截,且a∥b,若∠1=55°,则∠2等于( )
如图,直线a,b被直线c所截,且a∥b,若∠1=55°,则∠2等于( )| A. | 35° | B. | 45° | C. | 55° | D. | 125° |
20. 如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:$\sqrt{3}$,则大楼AB的高度约为( )(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)
如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:$\sqrt{3}$,则大楼AB的高度约为( )(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)
 如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:$\sqrt{3}$,则大楼AB的高度约为( )(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)
如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:$\sqrt{3}$,则大楼AB的高度约为( )(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)| A. | 30.6 | B. | 32.1 | C. | 37.9 | D. | 39.4 |
10.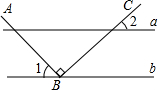 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,那么∠2的度数是( )
如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,那么∠2的度数是( )
 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,那么∠2的度数是( )
如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,那么∠2的度数是( )| A. | 20° | B. | 30° | C. | 35° | D. | 50° |
17.将0.00025用科学记数法表示为( )
| A. | 2.5×104 | B. | 0.25×10-4 | C. | 2.5×10-4 | D. | 25×10-5 |
14. 如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=80°,则∠1等于( )
如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=80°,则∠1等于( )
 如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=80°,则∠1等于( )
如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=80°,则∠1等于( )| A. | 120° | B. | 110° | C. | 100° | D. | 80° |
 ,则BC的长为( )
,则BC的长为( )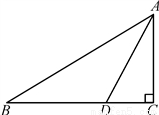
 +1 B.
+1 B.  +1
+1