题目内容
11.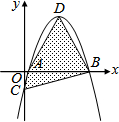 如图,坐标平面上,二次函数y=-x2+4x-k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?( )
如图,坐标平面上,二次函数y=-x2+4x-k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
分析 求出顶点和C的坐标,由三角形的面积关系得出关于k的方程,解方程即可.
解答 解:∵y=-x2+4x-k=-(x-2)2+4-k,
∴顶点D(2,4-k),C(0,-k),
∴OC=k,
∵△ABC的面积=$\frac{1}{2}$AB•OC=$\frac{1}{2}$AB•k,△ABD的面积=$\frac{1}{2}$AB(4-k),△ABC与△ABD的面积比为1:4,
∴k=$\frac{1}{4}$(4-k),
解得:k=$\frac{4}{5}$.
故选:D.
点评 本题考查了抛物线与x轴的交点、抛物线的顶点式;根据三角形的面积关系得出方程是解决问题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
1.6的相反数是( )
| A. | -6 | B. | $\frac{1}{6}$ | C. | -$\frac{1}{6}$ | D. | 6 |
6.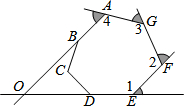 如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数为何?( )
如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数为何?( )
 如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数为何?( )
如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数为何?( )| A. | 40° | B. | 45° | C. | 50° | D. | 60° |
16. 如图,已知扇形AOB的半径为10公分,圆心角为54°,则此扇形面积为多少平方公分?( )
如图,已知扇形AOB的半径为10公分,圆心角为54°,则此扇形面积为多少平方公分?( )
 如图,已知扇形AOB的半径为10公分,圆心角为54°,则此扇形面积为多少平方公分?( )
如图,已知扇形AOB的半径为10公分,圆心角为54°,则此扇形面积为多少平方公分?( )| A. | 100π | B. | 20π | C. | 15π | D. | 5π |
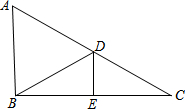 如图,△ABC中,D、E两点分别在AC、BC上,DE为BC的中垂线,BD为∠ADE的角平分线.若∠A=58°,则∠ABD的度数为何?( )
如图,△ABC中,D、E两点分别在AC、BC上,DE为BC的中垂线,BD为∠ADE的角平分线.若∠A=58°,则∠ABD的度数为何?( ) 如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:$\sqrt{3}$,则大楼AB的高度约为( )(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)
如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:$\sqrt{3}$,则大楼AB的高度约为( )(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)