题目内容
1.小昱和阿帆均从同一本书的第1页开始,逐页依顺序在每一页上写一个数.小昱在第1页写1,且之后每一页写的数均为他在前一页写的数加2;阿帆在第1页写1,且之后每一页写的数均为他在前一页写的数加7.若小昱在某页写的数为101,则阿帆在该页写的数为何?( )| A. | 350 | B. | 351 | C. | 356 | D. | 358 |
分析 根据题意确定出小昱和阿帆所写的数字,设小昱所写的第n个数为101,根据规律确定出n的值,即可确定出阿帆在该页写的数.
解答 解:小昱所写的数为 1,3,5,7,…,101,…;阿帆所写的数为 1,8,15,22,…,
设小昱所写的第n个数为101,
根据题意得:101=1+(n-1)×2,
整理得:2(n-1)=100,即n-1=50,
解得:n=51,
则阿帆所写的第51个数为1+(51-1)×7=1+50×7=1+350=351.
故选B
点评 此题考查了有理数的混合运算,弄清题中的规律是解本题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
12.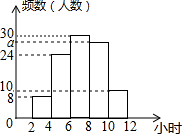 某校为了解全校同学五一假期参加社团活动的情况,抽查了100名同学,统计它们假期参加社团活动的时间,绘成频数分布直方图(如图),则参加社团活动时间的中位数所在的范围是( )
某校为了解全校同学五一假期参加社团活动的情况,抽查了100名同学,统计它们假期参加社团活动的时间,绘成频数分布直方图(如图),则参加社团活动时间的中位数所在的范围是( )
 某校为了解全校同学五一假期参加社团活动的情况,抽查了100名同学,统计它们假期参加社团活动的时间,绘成频数分布直方图(如图),则参加社团活动时间的中位数所在的范围是( )
某校为了解全校同学五一假期参加社团活动的情况,抽查了100名同学,统计它们假期参加社团活动的时间,绘成频数分布直方图(如图),则参加社团活动时间的中位数所在的范围是( )| A. | 4-6小时 | B. | 6-8小时 | C. | 8-10小时 | D. | 不能确定 |
16. 如图,已知扇形AOB的半径为10公分,圆心角为54°,则此扇形面积为多少平方公分?( )
如图,已知扇形AOB的半径为10公分,圆心角为54°,则此扇形面积为多少平方公分?( )
 如图,已知扇形AOB的半径为10公分,圆心角为54°,则此扇形面积为多少平方公分?( )
如图,已知扇形AOB的半径为10公分,圆心角为54°,则此扇形面积为多少平方公分?( )| A. | 100π | B. | 20π | C. | 15π | D. | 5π |
6.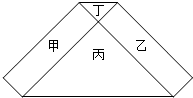 如图的六边形是由甲、乙两个长方形和丙、丁两个等腰直角三角形所组成,其中甲、乙的面积和等于丙、丁的面积和.若丙的一股长为2,且丁的面积比丙的面积小,则丁的一股长为何?( )
如图的六边形是由甲、乙两个长方形和丙、丁两个等腰直角三角形所组成,其中甲、乙的面积和等于丙、丁的面积和.若丙的一股长为2,且丁的面积比丙的面积小,则丁的一股长为何?( )
 如图的六边形是由甲、乙两个长方形和丙、丁两个等腰直角三角形所组成,其中甲、乙的面积和等于丙、丁的面积和.若丙的一股长为2,且丁的面积比丙的面积小,则丁的一股长为何?( )
如图的六边形是由甲、乙两个长方形和丙、丁两个等腰直角三角形所组成,其中甲、乙的面积和等于丙、丁的面积和.若丙的一股长为2,且丁的面积比丙的面积小,则丁的一股长为何?( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | 2-$\sqrt{3}$ | D. | 4-2$\sqrt{3}$ |
13. 如图,直线a,b被直线c所截,且a∥b,若∠1=55°,则∠2等于( )
如图,直线a,b被直线c所截,且a∥b,若∠1=55°,则∠2等于( )
 如图,直线a,b被直线c所截,且a∥b,若∠1=55°,则∠2等于( )
如图,直线a,b被直线c所截,且a∥b,若∠1=55°,则∠2等于( )| A. | 35° | B. | 45° | C. | 55° | D. | 125° |
10.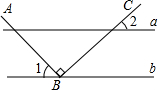 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,那么∠2的度数是( )
如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,那么∠2的度数是( )
 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,那么∠2的度数是( )
如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,那么∠2的度数是( )| A. | 20° | B. | 30° | C. | 35° | D. | 50° |
11.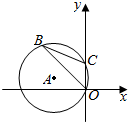 如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
 如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )| A. | $\frac{1}{3}$ | B. | 2$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{2\sqrt{2}}{3}$ |
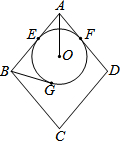 如图,菱形ABCD的边长为10,圆O分别与AB、AD相切于E、F两点,且与BG相切于G点.若AO=5,且圆O的半径为3,则BG的长度为何?( )
如图,菱形ABCD的边长为10,圆O分别与AB、AD相切于E、F两点,且与BG相切于G点.若AO=5,且圆O的半径为3,则BG的长度为何?( )