题目内容
8.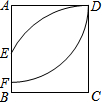 如图,以矩形ABCD的A为圆心,AD长为半径画弧,交AB于F点;再以C为圆心,CD长为半径画弧,交AB于E点.若AD=5,CD=$\frac{17}{3}$,则EF的长度为何?( )
如图,以矩形ABCD的A为圆心,AD长为半径画弧,交AB于F点;再以C为圆心,CD长为半径画弧,交AB于E点.若AD=5,CD=$\frac{17}{3}$,则EF的长度为何?( )| A. | 2 | B. | 3 | C. | $\frac{2}{3}$ | D. | $\frac{7}{3}$ |
分析 连接CE,可得出CE=CD,由矩形的性质得到BC=AD,在直角三角形BCE中,利用勾股定理求出BE的长,由AB-AF求出BF的长,由BE-BF求出EF的长即可.
解答 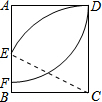 解:连接CE,则CE=CD=$\frac{17}{3}$,BC=AD=5,
解:连接CE,则CE=CD=$\frac{17}{3}$,BC=AD=5,
∵△BCE为直角三角形,
∴BE=$\sqrt{(\frac{17}{3})^{2}-{5}^{2}}$=$\frac{8}{3}$,
又∵BF=AB-AF=$\frac{17}{3}$-5=$\frac{2}{3}$,
∴EF=BE-BF=$\frac{8}{3}$-$\frac{2}{3}$=2.
故选A
点评 此题考查了矩形的性质,以及勾股定理,熟练掌握矩形的性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16. 如图,已知扇形AOB的半径为10公分,圆心角为54°,则此扇形面积为多少平方公分?( )
如图,已知扇形AOB的半径为10公分,圆心角为54°,则此扇形面积为多少平方公分?( )
 如图,已知扇形AOB的半径为10公分,圆心角为54°,则此扇形面积为多少平方公分?( )
如图,已知扇形AOB的半径为10公分,圆心角为54°,则此扇形面积为多少平方公分?( )| A. | 100π | B. | 20π | C. | 15π | D. | 5π |
13. 如图,直线a,b被直线c所截,且a∥b,若∠1=55°,则∠2等于( )
如图,直线a,b被直线c所截,且a∥b,若∠1=55°,则∠2等于( )
 如图,直线a,b被直线c所截,且a∥b,若∠1=55°,则∠2等于( )
如图,直线a,b被直线c所截,且a∥b,若∠1=55°,则∠2等于( )| A. | 35° | B. | 45° | C. | 55° | D. | 125° |
20. 如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:$\sqrt{3}$,则大楼AB的高度约为( )(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)
如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:$\sqrt{3}$,则大楼AB的高度约为( )(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)
 如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:$\sqrt{3}$,则大楼AB的高度约为( )(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)
如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:$\sqrt{3}$,则大楼AB的高度约为( )(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)| A. | 30.6 | B. | 32.1 | C. | 37.9 | D. | 39.4 |
17.将0.00025用科学记数法表示为( )
| A. | 2.5×104 | B. | 0.25×10-4 | C. | 2.5×10-4 | D. | 25×10-5 |
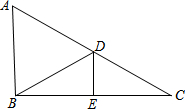 如图,△ABC中,D、E两点分别在AC、BC上,DE为BC的中垂线,BD为∠ADE的角平分线.若∠A=58°,则∠ABD的度数为何?( )
如图,△ABC中,D、E两点分别在AC、BC上,DE为BC的中垂线,BD为∠ADE的角平分线.若∠A=58°,则∠ABD的度数为何?( )