题目内容
6. 在平面直角坐标系中,一次函数y=ax+b(a≠0)的图形与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=$\frac{4}{3}$,点B的坐标为(m,-2).
在平面直角坐标系中,一次函数y=ax+b(a≠0)的图形与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=$\frac{4}{3}$,点B的坐标为(m,-2).(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.
分析 (1)根据正切函数,可得AH的长,根据勾股定理,可得AO的长,根据三角形的周长,可得答案;
(2)根据待定系数法,可得函数解析式.
解答 解:(1)由OH=3,tan∠AOH=$\frac{4}{3}$,得
AH=4.即A(-4,3).
由勾股定理,得
AO=$\sqrt{O{H}^{2}+A{H}^{2}}$=5,
△AHO的周长=AO+AH+OH=3+4+5=12;
(2)将A点坐标代入y=$\frac{k}{x}$(k≠0),得
k=-4×3=-12,
反比例函数的解析式为y=$\frac{-12}{x}$;
当y=-2时,-2=$\frac{-12}{x}$,解得x=6,即B(6,-2).
将A、B点坐标代入y=ax+b,得
$\left\{\begin{array}{l}{-4a+b=3}\\{6a+b=-2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=1}\end{array}\right.$,
一次函数的解析式为y=-$\frac{1}{2}$x+1.
点评 本题考查了反比例函数与一次函数的交点问题,利用待定系数法是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16. 如图,已知扇形AOB的半径为10公分,圆心角为54°,则此扇形面积为多少平方公分?( )
如图,已知扇形AOB的半径为10公分,圆心角为54°,则此扇形面积为多少平方公分?( )
 如图,已知扇形AOB的半径为10公分,圆心角为54°,则此扇形面积为多少平方公分?( )
如图,已知扇形AOB的半径为10公分,圆心角为54°,则此扇形面积为多少平方公分?( )| A. | 100π | B. | 20π | C. | 15π | D. | 5π |
17.将0.00025用科学记数法表示为( )
| A. | 2.5×104 | B. | 0.25×10-4 | C. | 2.5×10-4 | D. | 25×10-5 |
14. 如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=80°,则∠1等于( )
如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=80°,则∠1等于( )
 如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=80°,则∠1等于( )
如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=80°,则∠1等于( )| A. | 120° | B. | 110° | C. | 100° | D. | 80° |
11.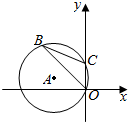 如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
 如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )| A. | $\frac{1}{3}$ | B. | 2$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{2\sqrt{2}}{3}$ |

 ,则BC的长为( )
,则BC的长为( )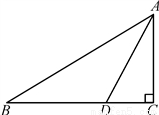
 +1 B.
+1 B.  +1
+1