题目内容
16.《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )| A. | x2-6=(10-x)2 | B. | x2-62=(10-x)2 | C. | x2+6=(10-x)2 | D. | x2+62=(10-x)2 |
分析 根据题意画出图形,设折断处离地面的高度为x尺,再利用勾股定理列出方程即可.
解答  解:如图,设折断处离地面的高度为x尺,则AB=10-x,BC=6,
解:如图,设折断处离地面的高度为x尺,则AB=10-x,BC=6,
在Rt△ABC中,AC2+BC2=AB2,即x2+62=(10-x)2.
故选D.
点评 本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图,领会数形结合的思想的应用.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
4.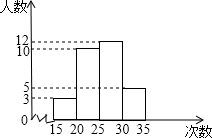 某校为了了解九年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在30~35次之间的频率是( )
某校为了了解九年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在30~35次之间的频率是( )
 某校为了了解九年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在30~35次之间的频率是( )
某校为了了解九年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在30~35次之间的频率是( )| A. | 0.2 | B. | 0.17 | C. | 0.33 | D. | 0.14 |
1.下列所述图形中,既是中心对称图形,又是轴对称图形的是( )
| A. | 正三角形 | B. | 平行四边形 | C. | 矩形 | D. | 正五边形 |
8.一幅美丽的图案,在某个顶点处由四个边长相等的正多边形镶嵌而成,其中的三个分别为正三边形,正四边形,正六边形,则另外一个为( )
| A. | 正三角形 | B. | 正四边形 | C. | 正五边形 | D. | 正六边形 |
6.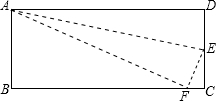 如图,在长方形ABCD中,DC=5cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC上,设此点为F,若△ABF的面积为30cm2,那么折叠△AED的面积为( )cm2.
如图,在长方形ABCD中,DC=5cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC上,设此点为F,若△ABF的面积为30cm2,那么折叠△AED的面积为( )cm2.
 如图,在长方形ABCD中,DC=5cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC上,设此点为F,若△ABF的面积为30cm2,那么折叠△AED的面积为( )cm2.
如图,在长方形ABCD中,DC=5cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC上,设此点为F,若△ABF的面积为30cm2,那么折叠△AED的面积为( )cm2.| A. | 16.9 | B. | 14.4 | C. | 13.5 | D. | 11.8 |