题目内容
11.在半径为1的⊙O中,弦AB、AC的长分别为1和$\sqrt{2}$,则∠BAC的度数为15°或105°.分析 根据题意画出图形,作出辅助线,由于AC与AB在圆心的同侧还是异侧不能确定,故应分两种情况进行讨论.
解答 解:分别作OD⊥AB,OE⊥AC,垂足分别是D、E.
∵OE⊥AC,OD⊥AB,
∴AE=$\frac{1}{2}$AC=$\frac{\sqrt{2}}{2}$,AD=$\frac{1}{2}$AB=$\frac{1}{2}$,
∴sin∠AOE=$\frac{AE}{AO}$=$\frac{\sqrt{2}}{2}$,sin∠AOD=$\frac{AD}{AO}$=$\frac{1}{2}$,
∴∠AOE=45°,∠AOD=30°,
∴∠BAO=60°,∠CAO=90°-45°=45°,
∴∠BAC=45°+60°=105°,或∠BAC′=60°-45°=15°.
∴∠BAC=15°或105°.
故答案是:15°或105°.
点评 本题考查的是垂径定理及直角三角形的性质,解答此题时进行分类讨论,不要漏解.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
2.下列计算正确的是( )
| A. | 3x-2x=1 | B. | (-a3)2=-a6 | C. | x6÷x2=x3 | D. | x3•x2=x5 |
16.《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
| A. | x2-6=(10-x)2 | B. | x2-62=(10-x)2 | C. | x2+6=(10-x)2 | D. | x2+62=(10-x)2 |
1.下列调查中,适宜采用全面调查方式的是( )
| A. | 了解长江中鱼的种类 | B. | 对“最强大脑”节目收视率的调查 | ||
| C. | 调查我国网名对某事件的看法 | D. | 对某班50名同学体重情况的调查 |
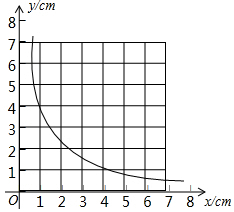 一个三角形的面积始终保持不变,它的一边的长为xcm,这边上的高为ycm,y与x的关系如图,根据图中给出的信息,解答下列问题:
一个三角形的面积始终保持不变,它的一边的长为xcm,这边上的高为ycm,y与x的关系如图,根据图中给出的信息,解答下列问题: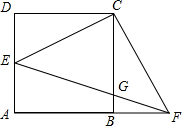 如图,四边形ABCD是边长为1的正方形,点E在AD边上运动,且不与点A和点D重合,连结CE,过点C作CF⊥CE交AB的延长线于点F,EF交BC于点G.
如图,四边形ABCD是边长为1的正方形,点E在AD边上运动,且不与点A和点D重合,连结CE,过点C作CF⊥CE交AB的延长线于点F,EF交BC于点G.