题目内容
已知二次函数y=2(x-3)2+1,则顶点坐标是 ;当x= 时,有最 值为 .
考点:二次函数的性质,二次函数的最值
专题:计算题
分析:直接根据二次函数的性质求解.
解答:解:二次函数y=2(x-3)2+1,顶点坐标是(3,1);当x=3时,有最小值为1.
故答案为(3,1),3,小,1.
故答案为(3,1),3,小,1.
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在菱形ABCD中,AB=6,∠A=30°,则菱形ABCD的面积为( )
在菱形ABCD中,AB=6,∠A=30°,则菱形ABCD的面积为( )| A、15 | B、18 | C、30 | D、60 |
下列四个函数中,是反比例函数的是( )
A、y=
| ||
B、y=
| ||
| C、y=3x-2 | ||
| D、y=x2 |
 点A是⊙O上一点,∠OCB=40°,则∠A的度数等于( )
点A是⊙O上一点,∠OCB=40°,则∠A的度数等于( )| A、60° | B、50° |
| C、40° | D、30° |

 如图,已知AD=AE,要使△ABD≌△ACE,应添加的条件是
如图,已知AD=AE,要使△ABD≌△ACE,应添加的条件是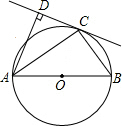 如图,AB是⊙O的直径,C是⊙O上一点,AD与过C点的切线互相垂直,垂足为D.
如图,AB是⊙O的直径,C是⊙O上一点,AD与过C点的切线互相垂直,垂足为D.