��Ŀ����
1���������Ԫһ�η�����$\left\{\begin{array}{l}2x+\begin{array}{l}{\begin{array}{l}{\;}��{y=3}\end{array}}\end{array}\\ \begin{array}{l}{\;}��{x+y=3}\end{array}\end{array}\right.$���ĵ�һ��������y��ϵ����ס���ڶ���������x��ϵ����ס������$\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$�����������Ľ⣬�������ԭ������������ ��y��ϵ��Ϊa��x��ϵ��Ϊb����$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$���뷽����$\left\{\begin{array}{l}{2x+ay=3}\\{bx+y=3}\end{array}\right.$�ó�$\left\{\begin{array}{l}{4+a=3}\\{2b+1=3}\end{array}\right.$�����������Ľ⣬���ɵó��𰸣�
��� �⣺��y��ϵ��Ϊa��x��ϵ��Ϊb��
��$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$���뷽����$\left\{\begin{array}{l}{2x+ay=3}\\{bx+y=3}\end{array}\right.$�ã�$\left\{\begin{array}{l}{4+a=3}\\{2b+1=3}\end{array}\right.$��
��ã�a=-1��b=1��
����ԭ������Ϊ$\left\{\begin{array}{l}2x-y=3\\ x+y=3\end{array}\right.$��
���� ���⿼���˶�Ԫһ�η�����Ľ⣬���Ԫһ�η������Ӧ�ã��������Ԫһ�η������Ķ����ǽ����Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
11�� ��ͼ���ȱߡ�ABC������BC����ƽ�Ƶ���DCE��λ�ã�����AD��BD�������н��ۣ�
��ͼ���ȱߡ�ABC������BC����ƽ�Ƶ���DCE��λ�ã�����AD��BD�������н��ۣ�
��AD=BC=CE��
��BD��AC����ƽ�֣�
���ı���ACED�����Σ�
���ı���ABED�����Ϊ$\frac{3\sqrt{3}}{4}$AB2��
������ȷ�ĸ����ǣ�������
 ��ͼ���ȱߡ�ABC������BC����ƽ�Ƶ���DCE��λ�ã�����AD��BD�������н��ۣ�
��ͼ���ȱߡ�ABC������BC����ƽ�Ƶ���DCE��λ�ã�����AD��BD�������н��ۣ���AD=BC=CE��
��BD��AC����ƽ�֣�
���ı���ACED�����Σ�
���ı���ABED�����Ϊ$\frac{3\sqrt{3}}{4}$AB2��
������ȷ�ĸ����ǣ�������
| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
9�����г��ȵĸ����߶������һ�������ε��ǣ�������
| A�� | 3cm��5cm��8cm | B�� | 1cm��2cm��3cm | C�� | 4cm��5cm��10cm | D�� | 3cm��4cm��5cm |
 ��ͼ��ij���尮����ѵ��ʱ��б��ʾ��ͼ�����ڰ�ȫ���ؿ��ǣ�������ѵ����б�µ������45�㽵Ϊ30�㣬��֪ԭб������AB�ij�Ϊ5�ף���D��B��C ��ͬһˮƽ�����ϣ�
��ͼ��ij���尮����ѵ��ʱ��б��ʾ��ͼ�����ڰ�ȫ���ؿ��ǣ�������ѵ����б�µ������45�㽵Ϊ30�㣬��֪ԭб������AB�ij�Ϊ5�ף���D��B��C ��ͬһˮƽ�����ϣ�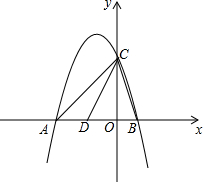 ��ͼ��������y=-x2-2x+3��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��
��ͼ��������y=-x2-2x+3��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��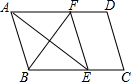 ��ͼ����ƽ���ı���ABCD�У���BAD��ƽ���߽�BC�ڵ�E����ABC��ƽ���߽�AD�ڵ�F����BF=12��AB=10����AE�ij�Ϊ��������
��ͼ����ƽ���ı���ABCD�У���BAD��ƽ���߽�BC�ڵ�E����ABC��ƽ���߽�AD�ڵ�F����BF=12��AB=10����AE�ij�Ϊ��������