题目内容
16.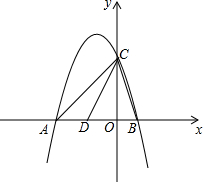 如图,抛物线y=-x2-2x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
如图,抛物线y=-x2-2x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.(1)求点A、B、C的坐标;
(2)设D为x轴上的任意一点(A点除外),当△DCB与△ACB相似时,求点D的坐标;
(3)若直线l过点P (4,0 ),Q为直线l上的动点,当以A、B、Q为顶点所作的直角三角形有且只有三个时,求直线l的解析式.
分析 (1)分别令x=0,y=0,即可解决问题、
(2)由△CBD∽△ABC,得$\frac{CB}{AB}$=$\frac{DB}{CB}$求出DB,即可解决问题.
(3)法一:如图2,过点A、B分别作x轴的垂线,这两条垂线与直线l总是有交点的,即2个点Q.以AB为直径的⊙G如果与直线l相交,那么就有2个点Q;如果圆与直线l相切,就只有1个点Q了,由题意可知直线l与⊙G相切于点Q,求出点Q坐标即可.
法二,求出点Q1坐标,即可解决问题.
解答 解:(1)令y=0,得x=-3或1,
∴抛物线与x轴的交点坐标为A(-3,0)、B(1,0);
令x=0,得y=3,
∴点C(0,3).
(2)如图,在Rt△BOC中,∵∠BOC=90°,BO=1,OC=3,
∴BC=$\sqrt{O{C}^{2}+O{C}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∵D为x轴上的任意一点(A点除外),△DCB与△ACB相似时
∴只有△CBD∽△ABC,
∴$\frac{CB}{AB}$=$\frac{DB}{CB}$,
∴DB=$\frac{C{B}^{2}}{AB}$=$\frac{10}{4}$=$\frac{5}{2}$,
∴OD=$\frac{3}{2}$,
故点D(-$\frac{3}{2}$,0),
(3)法一:如图2,过点A、B分别作x轴的垂线,这两条垂线与直线l总是有交点的,即2个点Q.
以AB为直径的⊙G如果与直线l相交,那么就有2个点Q;如果圆与直线l相切,就只有1个点Q了.
由题意可知直线l与⊙G相切于点Q,连结GQ,那么GQ⊥l.作QM⊥x轴于M,
在Rt△PGQ中,GQ=2,GP=5,所以PQ=$\sqrt{21}$.
则sin∠QGP=$\frac{\sqrt{21}}{5}$,cos$∠QGP=\frac{2}{5}$,
∵sin∠QGP=$\frac{QM}{QG}$=$\frac{\sqrt{21}}{5}$,
∴QM=$\frac{2\sqrt{21}}{5}$,
∵cos∠QGP=$\frac{GM}{QG}$=$\frac{2}{5}$,
∴GM=$\frac{4}{5}$,
∴OM=$\frac{1}{5}$,
∴点Q的坐标为($-\frac{1}{5}$,$\frac{{2\sqrt{21}}}{5}$),
∴直线l为y=-$\frac{2\sqrt{21}}{21}$x+$\frac{8\sqrt{21}}{21}$,
根据对称性,直线l还可以是$y=\frac{{2\sqrt{21}}}{21}x-\frac{{8\sqrt{21}}}{21}$.
(3)法二:如图2,过点A、B分别作x轴的垂线,这两条垂线与直线l总是有交点的,即2个点Q.
以AB为直径的⊙G如果与直线l相交,那么就有2个点Q;如果圆与直线l相切,就只有1个点Q了.
由题意可知直线l与⊙G相切于点Q,连结GQ,那么GQ⊥l.
在Rt△PGQ中,GQ=2,GP=5,所以PQ=$\sqrt{21}$.
由tan∠QPA=$\frac{GQ}{PQ}$=$\frac{A{Q}_{1}}{AP}$,得AQ1=$\frac{2\sqrt{21}}{3}$,
∴Q1(-3,$\frac{2\sqrt{21}}{3}$),
直线l为y=-$\frac{2\sqrt{21}}{21}$x+$\frac{8\sqrt{21}}{21}$,
根据对称性,直线l还可以是$y=\frac{{2\sqrt{21}}}{21}x-\frac{{8\sqrt{21}}}{21}$.
点评 本题考查二次函数综合题、相似三角形的判定和性质、锐角三角函数等知识,解题的关键是熟练掌握待定系数法确定函数解析式,学会添加常用辅助线,构造圆解决问题,学会正确画出图形利用三角函数解决,属于中考压轴题.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案| A. | 了解某校七年级(3)班的全体学生鞋子的尺码情况 | |
| B. | 了解河北卫视《看今朝》栏目的收视率 | |
| C. | 调查品牌牛奶的质量情况 | |
| D. | 调查磨山市居民的人均收入的情况 |
| A. | 3,4,5 | B. | 7,24,25 | C. | 1,$\sqrt{2}$,$\sqrt{3}$ | D. | 2,3,4 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. |  | B. |  | C. |  | D. |  |
| A. | x1=-1,x2=1 | B. | x1=-1,x2=2 | C. | x1=-2,x2=1 | D. | x1=-2,x2=2 |
