题目内容
6.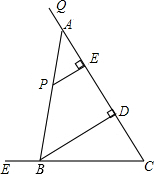 如图,tan∠QCF=2,点E在射线CQ上,CE=12,点P是∠QCF内一点,PE⊥QC于点E,PE=4,在射线CQ上取一点A,连AP并延长射线CF于点B,作BD⊥QC于点D.
如图,tan∠QCF=2,点E在射线CQ上,CE=12,点P是∠QCF内一点,PE⊥QC于点E,PE=4,在射线CQ上取一点A,连AP并延长射线CF于点B,作BD⊥QC于点D.(1)当AE的长度为多少时,△APE和△BDC相似;
(2)当点P是线段AB中点时,试判断△ABC的形状,并说明理由;
(3)连结BE,当S△APE=S△EBC时,求AE的长.
分析 (1)由AB⊥FC,PF⊥QC,得到∠APE=∠C,根据tan∠QCF=2,求得tan∠APE=2;由△APE∽△CBD,得到∠C=∠PAE,于是得到tan∠PAE=2,在Rt△APE中,PE=4,于是求得AE=$\frac{PE}{tan∠PAE}$=$\frac{4}{2}$=2,
(2)△ABC为直角三角形由PE∥BD,推出△APE∽△ABC,得到比例式$\frac{AP}{AB}$=$\frac{AE}{AD}$=$\frac{PE}{BD}$求得BD=8,CD=4,通过△APE∽△BCD,得到∠DBC=∠PAE,于是得到∠ABC=∠ABD+∠DBC=∠ABD+∠BAD=90°,从而证得结论;
(3)如图,连接BE,设DC=a,则BD=2a,得到S△APE=S△EBC,=12a,由△APE∽△ABD,得到比例式$\frac{PE}{BD}$=$\frac{AE}{AD}$,解方程$\frac{4}{2a}$=$\frac{6a}{6a+12-a}$,即可得到结果.
解答 解:(1)∵AB⊥FC,PF⊥QC,
∴∠APE=∠C,
∵tan∠QCF=2,
∴tan∠APE=2.
∵△APE∽△CBD,
∴∠C=∠PAE,
∴tan∠PAE=2,
在Rt△APE中,PE=4,
∴AE=$\frac{PE}{tan∠PAE}$=$\frac{4}{2}$=2;
(2)△ABC为直角三角形,理由如下:
∵PE∥BD,
∴△APE∽△ABC,
∴$\frac{AP}{AB}$=$\frac{AE}{AD}$=$\frac{PE}{BD}$.
∵点P是线段AB中点,
∴$\frac{AP}{AB}$=$\frac{AE}{AD}$=$\frac{PE}{BD}$=$\frac{1}{2}$.
∵PE=4,
∴BD=8,
∴CD=4,
∴DE=12-4=8,
∴AE=8,
∵$\frac{AE}{BD}$=$\frac{PE}{CD}$=1,∠AEP=∠BDF,
∴△APE∽△BCD,
∴∠DBC=∠PAE,
∴∠ABC=∠ABD+∠DBC=∠ABD+∠BAD=90°,
∴△ABC是直角三角形;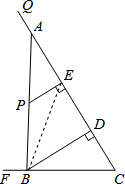 (4)如图,连接BE,设DC=a,则BD=2a,
(4)如图,连接BE,设DC=a,则BD=2a,
∴S△EBC=12a,
∵S△APE=S△EBC,=12a,
∵PE=4,
∴AE=6a,
∵△APE∽△ABD,
∴$\frac{PE}{BD}$=$\frac{AE}{AD}$,即 $\frac{4}{2a}$=$\frac{6a}{6a+12-a}$,
解得:a=3(负值舍去),
∴AE=18.
点评 本题主要考查了相似三角形的判定与性质,锐角三角函数的定义,三角形的面积,三角形中位线定理,综合性较强,有一定难度.进行分类讨论是解决第一问的关键.

 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案 函数y=x2+2x-3的图象如图所示,当x=m时,y<0,则m的值可能是( )
函数y=x2+2x-3的图象如图所示,当x=m时,y<0,则m的值可能是( )| A. | -4 | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
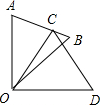 如图,△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,∠AOD=90°,求∠A和∠B的度数.
如图,△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,∠AOD=90°,求∠A和∠B的度数.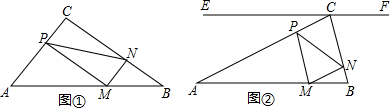
 根据要求设计一种方案(包括画出相应的图形.指出需要测量的线段等).
根据要求设计一种方案(包括画出相应的图形.指出需要测量的线段等). 已知x轴上两点A(-1,0)、B(4,0).
已知x轴上两点A(-1,0)、B(4,0).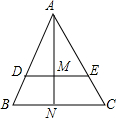 如图,已知△ABC中,DE∥BC,DE=8,BC=12,AN⊥BC交DE于M,四边形BCED的面积为90.求△ADE的面积及AM、AN的长.
如图,已知△ABC中,DE∥BC,DE=8,BC=12,AN⊥BC交DE于M,四边形BCED的面积为90.求△ADE的面积及AM、AN的长.