题目内容
1.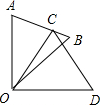 如图,△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,∠AOD=90°,求∠A和∠B的度数.
如图,△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,∠AOD=90°,求∠A和∠B的度数.
分析 先根据旋转的性质得∠AOC=∠BOD=40°,OA=OC,则根据等腰三角形的性质和三角形内角和定理可计算出∠A=$\frac{1}{2}$(180°-∠A)=70°,再利用互余计算出∠AOB=90°-∠BOD=50°,然后在△AOB中利用三角形内角和计算∠B的度数.
解答 解:∵△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,
∴∠AOC=∠BOD=40°,OA=OC,
∵OA=OC,
∴∠A=∠OCA,
∴∠A=$\frac{1}{2}$(180°-40°)=70°,
∵∠AOD=90°,
∴∠AOB=90°-∠BOD=50°,
在△AOB中,∠B=180°-∠A-∠AOB=180°-70°-50°=60°.
答:∠A和∠B的度数分别为70°,60°.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.本题的关键是灵活应用等腰三角形的性质.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
3.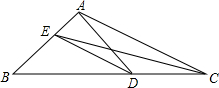 如图,在△ABC中,点D是BC上的一点,已知∠DAC=30°,∠DAB=75°,CE平分∠ACB交AB于点E,连接DE,则∠DEC=( )
如图,在△ABC中,点D是BC上的一点,已知∠DAC=30°,∠DAB=75°,CE平分∠ACB交AB于点E,连接DE,则∠DEC=( )
 如图,在△ABC中,点D是BC上的一点,已知∠DAC=30°,∠DAB=75°,CE平分∠ACB交AB于点E,连接DE,则∠DEC=( )
如图,在△ABC中,点D是BC上的一点,已知∠DAC=30°,∠DAB=75°,CE平分∠ACB交AB于点E,连接DE,则∠DEC=( )| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
 若二次函数y=ax2+bx+c的图象如图所示,则它的对称轴是x=3.
若二次函数y=ax2+bx+c的图象如图所示,则它的对称轴是x=3.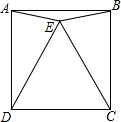 如图,四边形ABCD是正方形,△CDE是等边三角形,若AE=4cm,则S△AEB=4cm2.
如图,四边形ABCD是正方形,△CDE是等边三角形,若AE=4cm,则S△AEB=4cm2. 我们规定,是函数值为零的x的值称为函数的零点,例如函数y=x-1,令y=0,可得x=1,则我们就说1是函数y=x-1的零点.
我们规定,是函数值为零的x的值称为函数的零点,例如函数y=x-1,令y=0,可得x=1,则我们就说1是函数y=x-1的零点.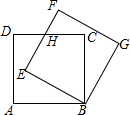 已知如图边长为1cm的两个正方形互相重合,按住其中一个不动,将另一个绕顶点B顺时针旋转30°,则这两个正方形重叠部分的面积是$\frac{\sqrt{3}}{3}$cm2.
已知如图边长为1cm的两个正方形互相重合,按住其中一个不动,将另一个绕顶点B顺时针旋转30°,则这两个正方形重叠部分的面积是$\frac{\sqrt{3}}{3}$cm2.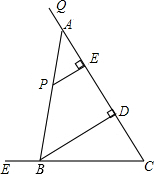 如图,tan∠QCF=2,点E在射线CQ上,CE=12,点P是∠QCF内一点,PE⊥QC于点E,PE=4,在射线CQ上取一点A,连AP并延长射线CF于点B,作BD⊥QC于点D.
如图,tan∠QCF=2,点E在射线CQ上,CE=12,点P是∠QCF内一点,PE⊥QC于点E,PE=4,在射线CQ上取一点A,连AP并延长射线CF于点B,作BD⊥QC于点D.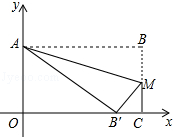 矩形OABC在平面直角坐标系中的位置如图所示,O为坐标原点,OA与y轴重合,OC与x轴重合,M为BC上点,沿AM折叠矩形使得点B′落在OC上,且知
矩形OABC在平面直角坐标系中的位置如图所示,O为坐标原点,OA与y轴重合,OC与x轴重合,M为BC上点,沿AM折叠矩形使得点B′落在OC上,且知