题目内容
18. 已知x轴上两点A(-1,0)、B(4,0).
已知x轴上两点A(-1,0)、B(4,0).(1)在y轴上取一点C,使∠ACB=90°,则点C的坐标为(0,2)或(0,-2).
(2)设点$D({x,-\frac{1}{2}{x^2}+\frac{3}{2}x+2})$是平面直角坐标系xOy中的一个动点,以AB为斜边的直角三角形ADB与△AOC相似时,求D点坐标.
(3)设动点$D({x,-\frac{1}{2}{x^2}+\frac{3}{2}x+2})$到x轴的距离为h,当h≥OC时,求x的取值范围.
分析 (1)设C(0,y),根据勾股定理和两点间的距离公式进行解答;
(2)需要分类讨论:①当∠ADB=90°2时,过D作DH⊥x轴,则△AOC∽△ADB∽△AHD,结合相似三角形的对应边成比例求得x的值;
②当∠ADB=90°时,同理可得$\frac{AO}{CO}=\frac{DH}{AH}=\frac{1}{2}$,结合相似三角形的对应边成比例求得x的值;
(3)根据函数的性质得到|h|≥2,由此求得相应的x的取值范围.
解答 解:(1)设C(0,y),则
12+y2+42+y2=52,
解得y=±2,
故点C的坐标为:(0,2)或(0,-2).
故答案是:(0,2)或(0,-2);
(2)依题意得AO=1,OC=2,AB=4-(-1)=5.
∵y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=-$\frac{1}{2}$(x-4)(x+1),
∴该抛物线与x轴的交点坐标是A(-1,0)、B(4,0),
即抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2经过点A、B、D.
以AB为斜边的直角三角形有下列情况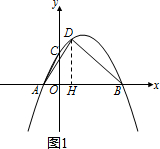
①如图1,当∠ADB=90°时,过D作DH⊥x轴,则△AOC∽△ADB∽△AHD,
∴$\frac{AO}{CO}=\frac{AH}{DH}=\frac{1}{2}$
则有$\frac{{-\frac{1}{2}{x^2}+\frac{3}{2}x+2}}{x-(-1)}=2$,解得x1=-1(舍去),x2=0,
∴D1(0,2);
②当∠ADB=90°时,同理可得$\frac{AO}{CO}=\frac{DH}{AH}=\frac{1}{2}$
同理可得$\frac{{-\frac{1}{2}{x^2}+\frac{3}{2}x+2}}{x-(-1)}=\frac{1}{2}$,解得x3=-1,x4=3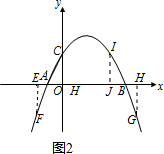
∴D2(3,2);
综上所述点D1(0,2)和点D2(3,2)符合要求;
(3)令$-\frac{1}{2}{x^2}+\frac{3}{2}x+2=2$得:x1=3,x2=0;
令$-\frac{1}{2}{x^2}+\frac{3}{2}x+2=-2$得:${x_3}=\frac{{3+\sqrt{41}}}{2}$,${x_4}=\frac{{3-\sqrt{41}}}{2}$;
令$y=-\frac{1}{2}{x^2}+\frac{3}{2}x+2$,可得该函数图象如图所示2,
当$x≤\frac{{3-\sqrt{41}}}{2}$或$x≥\frac{{3+\sqrt{41}}}{2}$或0≤x≤3时,h≥OC.
点评 本题综合考查了相似三角形的判定与性质,二次函数图象上点的坐标特征,二次函数最值的求法以及勾股定理的应用等知识点,综合性比较强,另外,解答有关于动点问题时,必须分类讨论,以防漏解或错解.

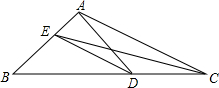 如图,在△ABC中,点D是BC上的一点,已知∠DAC=30°,∠DAB=75°,CE平分∠ACB交AB于点E,连接DE,则∠DEC=( )
如图,在△ABC中,点D是BC上的一点,已知∠DAC=30°,∠DAB=75°,CE平分∠ACB交AB于点E,连接DE,则∠DEC=( )| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
| A. | 8 | B. | 10 | C. | 8或10 | D. | 12 |
 我们规定,是函数值为零的x的值称为函数的零点,例如函数y=x-1,令y=0,可得x=1,则我们就说1是函数y=x-1的零点.
我们规定,是函数值为零的x的值称为函数的零点,例如函数y=x-1,令y=0,可得x=1,则我们就说1是函数y=x-1的零点.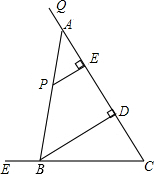 如图,tan∠QCF=2,点E在射线CQ上,CE=12,点P是∠QCF内一点,PE⊥QC于点E,PE=4,在射线CQ上取一点A,连AP并延长射线CF于点B,作BD⊥QC于点D.
如图,tan∠QCF=2,点E在射线CQ上,CE=12,点P是∠QCF内一点,PE⊥QC于点E,PE=4,在射线CQ上取一点A,连AP并延长射线CF于点B,作BD⊥QC于点D.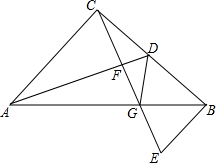 如图所示,△ABC是等腰直角三角形,CA=CB,∠ACB=90°,AD是BC边上的中线,过C作AD的垂线,垂足为F,交AB于点G,过点B作BE⊥BC,交CG的延长线于点E,连接DG.
如图所示,△ABC是等腰直角三角形,CA=CB,∠ACB=90°,AD是BC边上的中线,过C作AD的垂线,垂足为F,交AB于点G,过点B作BE⊥BC,交CG的延长线于点E,连接DG.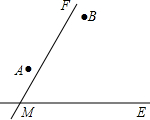 两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部.
两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部.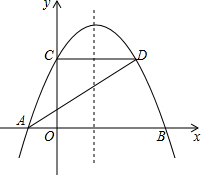 如图,已知抛物线y=ax2+$\frac{4}{3}$x+c与x轴交于A、B两点,与y轴交于点C,点D在抛物线上,且A(-1,0),D(2,2).
如图,已知抛物线y=ax2+$\frac{4}{3}$x+c与x轴交于A、B两点,与y轴交于点C,点D在抛物线上,且A(-1,0),D(2,2).