题目内容
4.用适当的方法解下列方程:(1)(x+1)2-9=0
(2)x2-2x=3
(3)2(x-1)2=3x-3.
(4)3x2+4x-1=0.
分析 (1)直接开平方法求解即可;
(2)因式分解法求解可得;
(3)因式分解法求解可得;
(4)公式法求解可得.
解答 解:(1)(x+1)2=9,
x+1=±3,即x+1=3或x+1=-3,
解得:x1=2,x2=-4;
(2)x2-2x-3=0,
因式分解可得:(x+1)(x-3)=0,
∴x+1=0或x-3=0,
解得:x1=3,x2=-1;
(3)2(x-1)2-3(x-1)=0,
(x-1)[2(x-1)-3]=0,即(x-1)(2x-5)=0,
∴x-1=0或2x-5=0,
解得:x=1或x=$\frac{5}{2}$;
(4)∵a=3,b=4,c=-1,
∴b2-4ac=16+12=28>0,
∴x=$\frac{4±\sqrt{28}}{6}$=$\frac{4±2\sqrt{7}}{6}$=$\frac{2±\sqrt{7}}{3}$,
∴x1=$\frac{-2+\sqrt{7}}{3}$,x2=$\frac{-2-\sqrt{7}}{3}$.
点评 本题主要考查解一元二次方程的能力,根据不同的方程选择合适的方法是解题的关键.

练习册系列答案
相关题目
14.在△ABC中,CD是AB上的高.由下列条件不一定能推出∠ACB=90°的是( )
| A. | ∠B+∠ACD=90° | B. | CD2=AD•DB | C. | $\frac{AC}{BC}$=$\frac{CD}{DB}$ | D. | ∠A=∠DCB |
15.用指定方法解下列一元二次方程.
(1)x2-36=0 (直接开平方法)
(2)x2-4x=2(配方法)
(3)2x2-5x+1=0(公式法)
(4)(x+1)2+8(x+1)+16=0(因式分解法)
(1)x2-36=0 (直接开平方法)
(2)x2-4x=2(配方法)
(3)2x2-5x+1=0(公式法)
(4)(x+1)2+8(x+1)+16=0(因式分解法)
19.下列标志中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,在△ABC中,∠ACB=90°,BC=3cm,AC=4cm,D是AB的中点,若以点C为圆心,以3cm长为半径作⊙C,则下列选项中的点在⊙C外的是( )
如图,在△ABC中,∠ACB=90°,BC=3cm,AC=4cm,D是AB的中点,若以点C为圆心,以3cm长为半径作⊙C,则下列选项中的点在⊙C外的是( )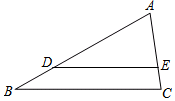 如图,在△ABC中,点D、E分别在AB、AC边上,且DE∥BC,若AD:DB=3:1,AE=6,则AC等于( )
如图,在△ABC中,点D、E分别在AB、AC边上,且DE∥BC,若AD:DB=3:1,AE=6,则AC等于( )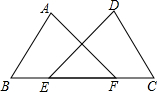 如图,点E、F在线段BC上且F在E的右侧,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.
如图,点E、F在线段BC上且F在E的右侧,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.