题目内容
14.在△ABC中,CD是AB上的高.由下列条件不一定能推出∠ACB=90°的是( )| A. | ∠B+∠ACD=90° | B. | CD2=AD•DB | C. | $\frac{AC}{BC}$=$\frac{CD}{DB}$ | D. | ∠A=∠DCB |
分析 A.错误.无法证明∠ACB=90°.
B、正确.只要证明△ADC∽△CDB,推出∠ACD=∠B,由∠B+∠DCB=90°推出∠ACD+∠DCB=90°即可证明.
C、正确.只要证明△DBC∽△CBA,推出∠ACB=∠BDC即可.
D、正确..由∠A=∠DCB,∠A+∠ACD=90°,推出∠ACD+∠DCB=90°即可证明.
解答 解:A、错误.∵∠B+∠ACD=90°,∠B+∠DCB=90°,
∴∠ACD=∠DCB,推不出∠ACB=90°.
B、正确.∵CD2=AD•DB,
∴$\frac{CD}{AD}$=$\frac{DB}{CD}$,∵∠ADC=∠BDC=90°,
∴△ADC∽△CDB,
∴∠ACD=∠B,
∵∠B+∠DCB=90°,
∴∠ACD+∠DCB=90°,
∴∠ACB=90°.
C、正确.∵$\frac{AC}{BC}$=$\frac{CD}{DB}$,∠B=∠B,
∴△DBC∽△CBA,
∴∠ACB=∠BDC=90°
D、正确.∵∠A=∠DCB,∠A+∠ACD=90°,
∴∠ACD+∠DCB=90°,
∴∠ACB=90°
故选A.
点评 本题考查相似三角形的性质、等角的余角相等等知识,解题的关键是熟练掌握相似三角形的判定和性质,属于中考常考题型.

练习册系列答案
相关题目
11.下列各组中是同类项的是( )
| A. | 3x2y与2xy2 | B. | $\frac{1}{3}$x4y与$\frac{1}{2}$yx4 | ||
| C. | -2a与0 | D. | $\frac{1}{2}$πa2bc3与-3a2cb3 |
5.某公司员工分别住在A、B、C、D四个住宅区,A区有20人,B区有15人,C区有5人,D区有30人,四个区在同一条直线上,位置如图所示.该公司的接送车打算在此间设立一个停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠点的位置应设置在( )
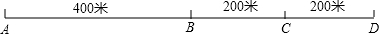
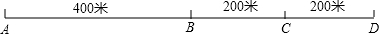
| A. | D区 | B. | A区 | C. | AB两区之间 | D. | BC两区之间 |
2.在(-4)-( )=-9中的括号里应填( )
| A. | -5 | B. | 5 | C. | 13 | D. | -13 |
9.下列所列代数式正确的是( )
| A. | a与b的积的立方是ab3 | B. | x与y的平方差是(x-y)2 | ||
| C. | x与y的倒数的差是x-$\frac{1}{y}$ | D. | x与5的差的7倍是7x-5 |
3.下列等式中,不一定成立的是( )
| A. | $\sqrt{2\frac{2}{3}}$=2$\sqrt{\frac{2}{3}}$ | B. | $\frac{1}{a+b}=\frac{c}{(a+b)c}$ | C. | a$\sqrt{-\frac{1}{a}}$=-$\sqrt{-a}$ | D. | $\frac{-c}{-a+b}=\frac{c}{a-b}$ |