题目内容
15.用指定方法解下列一元二次方程.(1)x2-36=0 (直接开平方法)
(2)x2-4x=2(配方法)
(3)2x2-5x+1=0(公式法)
(4)(x+1)2+8(x+1)+16=0(因式分解法)
分析 (1)直接开平方法求解;
(2)配方法求解可得;
(3)公式法求解即可;
(4)因式分解法解之可得.
解答 解:(1)x2=36,
∴x=±6,
即x1=-6,x2=6;
(2)x2-4x+4=2+4,即(x-2)2=6,
∴x-2=$±\sqrt{6}$,
∴x1=2-$\sqrt{6}$,x2=2+$\sqrt{6}$;
(3)∵a=2,b=-5,c=1,
∴b2-4ac=25-8=17>0,
∴x=$\frac{5±\sqrt{17}}{4}$,
即x1=$\frac{5-\sqrt{17}}{4}$,x2=$\frac{5+\sqrt{17}}{4}$;
(4)(x+1+4)2=0,即(x+5)2=0,
∴x+5=0,
即x1=x2=-5.
点评 本题主要考查解一元二次方程的能力,根据不同的方程选择合适的方法是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.某公司员工分别住在A、B、C、D四个住宅区,A区有20人,B区有15人,C区有5人,D区有30人,四个区在同一条直线上,位置如图所示.该公司的接送车打算在此间设立一个停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠点的位置应设置在( )
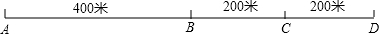
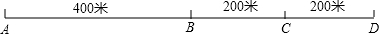
| A. | D区 | B. | A区 | C. | AB两区之间 | D. | BC两区之间 |
3.下列等式中,不一定成立的是( )
| A. | $\sqrt{2\frac{2}{3}}$=2$\sqrt{\frac{2}{3}}$ | B. | $\frac{1}{a+b}=\frac{c}{(a+b)c}$ | C. | a$\sqrt{-\frac{1}{a}}$=-$\sqrt{-a}$ | D. | $\frac{-c}{-a+b}=\frac{c}{a-b}$ |
20.如果有理数a,b使得$\frac{a+18}{b-18}$=0,那么( )
| A. | a-b2是负数 | B. | a-b是负数 | C. | a+b2是正数 | D. | a+b是正数 |
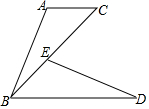 如图,点E在BC上,AC∥BD,AC=BE,BC=BD.
如图,点E在BC上,AC∥BD,AC=BE,BC=BD.


