题目内容
12．
如图，在△ABC中，∠ACB=90°，BC=3cm，AC=4cm，D是AB的中点，若以点C为圆心，以3cm长为半径作⊙C，则下列选项中的点在⊙C外的是（ ）| A． | 点A | B． | 点B | C． | 点C | D． | 点D |
分析 分别求出AB、CD的长，根据点与圆的位置关系的判断方法进行判断即可．
解答 解：∵∠C=90°，BC=3cm，AC=4cm，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5，
∵以点C为圆心，以3cm长为半径作⊙C，
∴点A在⊙C外，
∵D是AB的中点，
∴CD=$\frac{1}{2}$AB=2.5，
故D在圆C内部，B在圆上，C是圆心．
故选：A．
点评 本题考查的是点与圆的位置关系的判断．关键要记住若半径为r，点到圆心的距离为d，则有：当d＞r时，点在圆外；当d=r时，点在圆上，当d＜r时，点在圆内．
练习册系列答案
相关题目
2．在（-4）-（ ）=-9中的括号里应填（ ）
| A． | -5 | B． | 5 | C． | 13 | D． | -13 |
3．下列等式中，不一定成立的是（ ）
| A． | $\sqrt{2\frac{2}{3}}$=2$\sqrt{\frac{2}{3}}$ | B． | $\frac{1}{a+b}=\frac{c}{（a+b）c}$ | C． | a$\sqrt{-\frac{1}{a}}$=-$\sqrt{-a}$ | D． | $\frac{-c}{-a+b}=\frac{c}{a-b}$ |
20．如果有理数a，b使得$\frac{a+18}{b-18}$=0，那么（ ）
| A． | a-b2是负数 | B． | a-b是负数 | C． | a+b2是正数 | D． | a+b是正数 |
17．下列说法不正确的是（ ）
| A． | 全等三角形对应角平分线相等，对应边上的高、中线也分别相等 | |
| B． | 全等三角形的周长和面积都相等 | |
| C． | 全等三角形的对应角相等，对应边相等 | |
| D． | 全等三角形是指周长和面积都相等的三角形 |
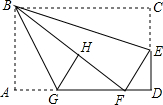如图，在矩形纸片ABCD中，AB=6，BC=10，点E在CD上，将△BCE沿BE折叠，点C恰落在边AD上的点F处；点G在AF上，将△ABG沿BG折叠，点A恰落在线段BF上的点H处，①∠EBG=45°；②△DEF∽△ABG；③S△ABG=$\frac{3}{2}$S△FGH；④AG+DF=FG．则下列结论正确的有（ ）
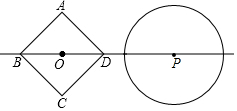如图，正方形ABCD的边长为$\sqrt{2}$，⊙P的半径为1，正方形ABCD的中心O和⊙P的圆心P都在直线l上，线段OP的长叫做它们的中心距，⊙P随着点P在直线l上的运动而运动．