题目内容
10.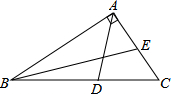 如图,在△ABC中,∠BAC=90°,AD是角平分线,BE是中线,则下列结论:
如图,在△ABC中,∠BAC=90°,AD是角平分线,BE是中线,则下列结论:①BD=CD;②∠DAB=45°;③∠ABE=∠CBE;④∠ABC+∠ACB=90°;⑤S△ABC=S△ABE.
其中所有正确的结论是②④(只填写序号)
分析 根据角平分线的定义、中线的定义、三角形内角和定理判断即可.
解答 解:∵AD是角平分线,
∴BD与CD不一定相等,①错误;
∵∠BAC=90°,AD是角平分线,
∴∠DAB=$\frac{1}{2}$∠BAC=45°,②正确;
∵BE是中线,
∴∠ABE与∠CBE不一定相等,③错误;
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,④正确;
由图形可知,S△ABC>S△ABE,⑤错误,
故答案为:②④.
点评 本题考查的是角平分线的性质、三角形的中线的性质以及三角形内角和定理的应用,熟记角平分线的性质、三角形的中线的性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.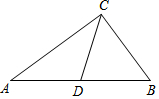 已知Rt△ABC中,∠ACB=90°,∠B=54°,CD是斜边AB上的中线,则∠ACD的度数是( )
已知Rt△ABC中,∠ACB=90°,∠B=54°,CD是斜边AB上的中线,则∠ACD的度数是( )
 已知Rt△ABC中,∠ACB=90°,∠B=54°,CD是斜边AB上的中线,则∠ACD的度数是( )
已知Rt△ABC中,∠ACB=90°,∠B=54°,CD是斜边AB上的中线,则∠ACD的度数是( )| A. | 18° | B. | 36° | C. | 54° | D. | 72° |
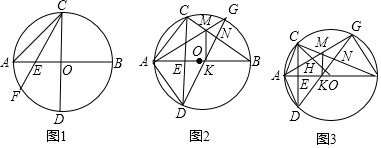
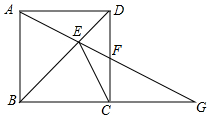 如图,ABCD是正方形,G是BC延长线上一点,AG交BD于E,交CD于F,求证:CE与△CFG的外接圆相切.
如图,ABCD是正方形,G是BC延长线上一点,AG交BD于E,交CD于F,求证:CE与△CFG的外接圆相切.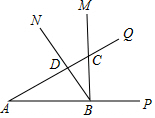 如图,∠PAQ=∠MBN=30°,∠MBN的顶点B在射线AP上,射线BM和射线BN分别交射线AQ于点C、D,当∠MBN绕点B转动时.若AB=2$\sqrt{3}$,则CA•CD的最小值是( )
如图,∠PAQ=∠MBN=30°,∠MBN的顶点B在射线AP上,射线BM和射线BN分别交射线AQ于点C、D,当∠MBN绕点B转动时.若AB=2$\sqrt{3}$,则CA•CD的最小值是( )